Deletion in a linked list

Deleting a node in a linked list

Consider the following linked list:

Deletion in this list can be divided into the following categories.

Case 1: Deleting the first node.
Case 2: Deleting the node at the index.
Case 3: Deleting the last node.
Case 4: Deleting a node with a given value.

For deletion, follwoing any of the above-mentioned cases, we would just need to free that extra node left after we disconnect it from the list.
Before that, we overwrite the current connection and make new connections. And that is how we delete a node from our desired place.

Syntax of freeing a node → free(ptr);
The above syntax will free this node, that is, remove its reserved location in the heap.
Now, let's begin with each of these cases of insertion.

Deleting the first node

In order to delete the node at the beginning, we would need to have the head pointer pointer to the node second to the head node, that is, head->next. And we would simple free the node that's left.

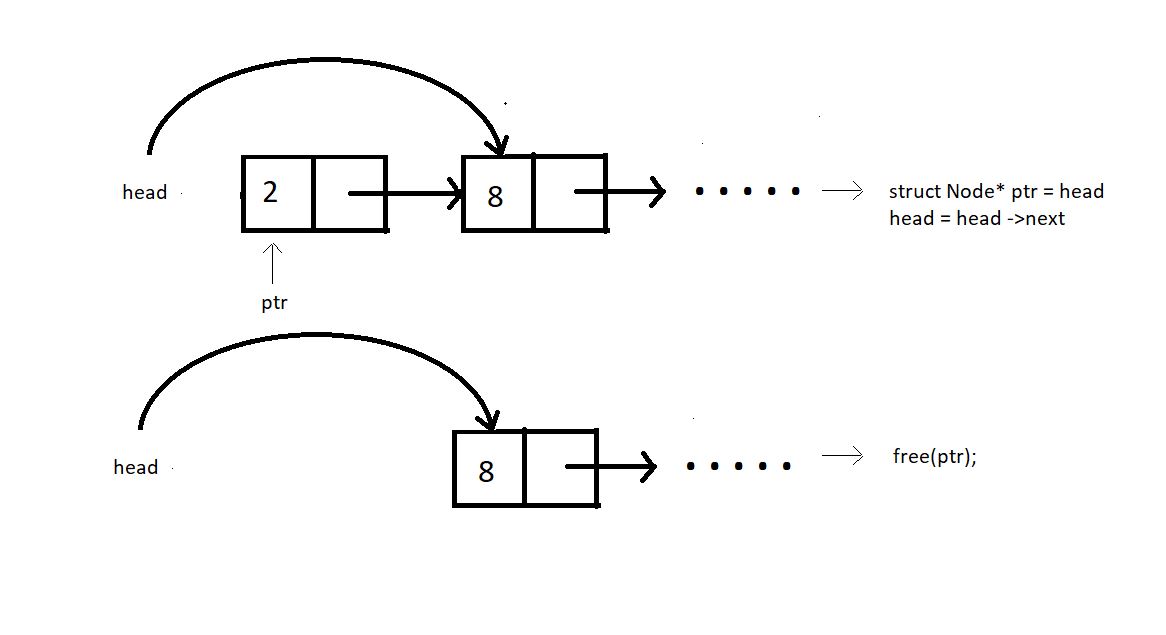
struct Node * deleteFirst
(struct Node * head){
struct Node * ptr = head;
head = head->next;
free(ptr);
return head;
}

Deleting at some index in between:

Assuming index starts from 0, we can delete an element from index i>0 as follows:
Bring a temporary pointer p pointing to the node before the element you wan to delete in the linked list.
Since we want to delete between 2 and 8, we bring pointer p to 2.
Assuming ptr points at the element we want to delete.
We make pointer p point to the next node after pointer ptr skipping ptr.
We can now free the pointer skipped.

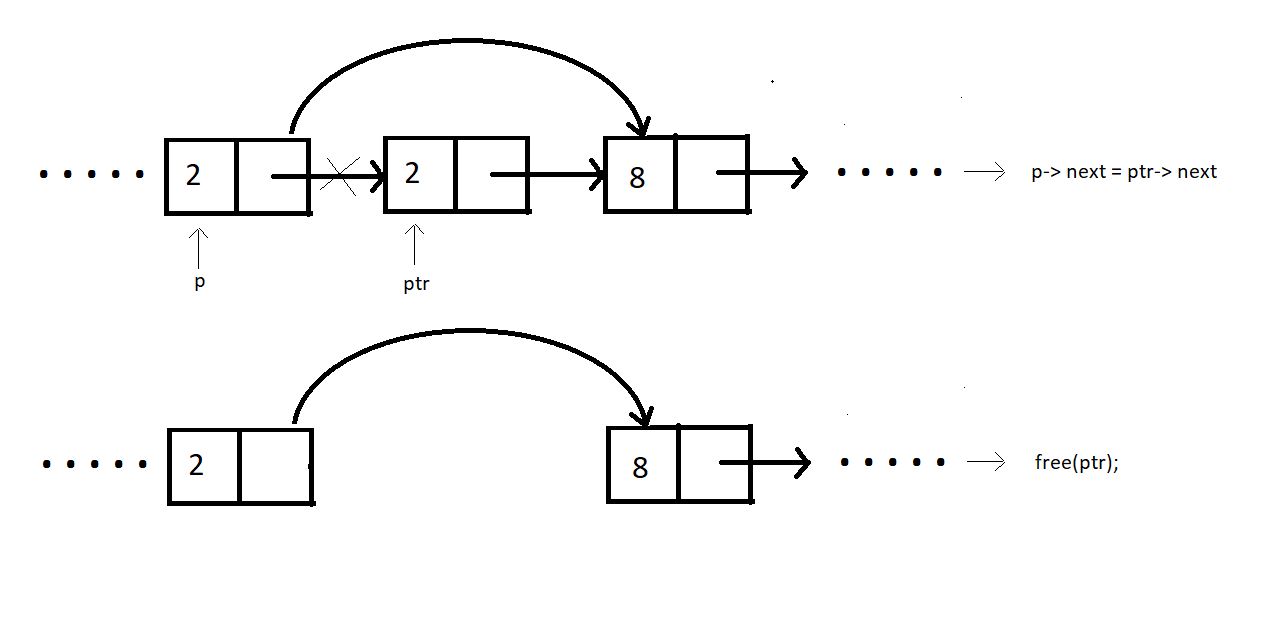
struct Node * deleteAtIndex(struct Node * head, int index){
struct Node *p = head;
struct Node *q = head->next;
for (int i = 0; i < index-1; i++)
{
p = p->next;
q = q->next;
}

p->next = q->next;
free(q);
return head;
}

Deleting at the end.

In order to delete an element at the end of the linked list, we bring a temporary pointer ptr to the last element. And a pointer p to the second last. We make the second last element to point at NULL. And we free the pointer ptr.

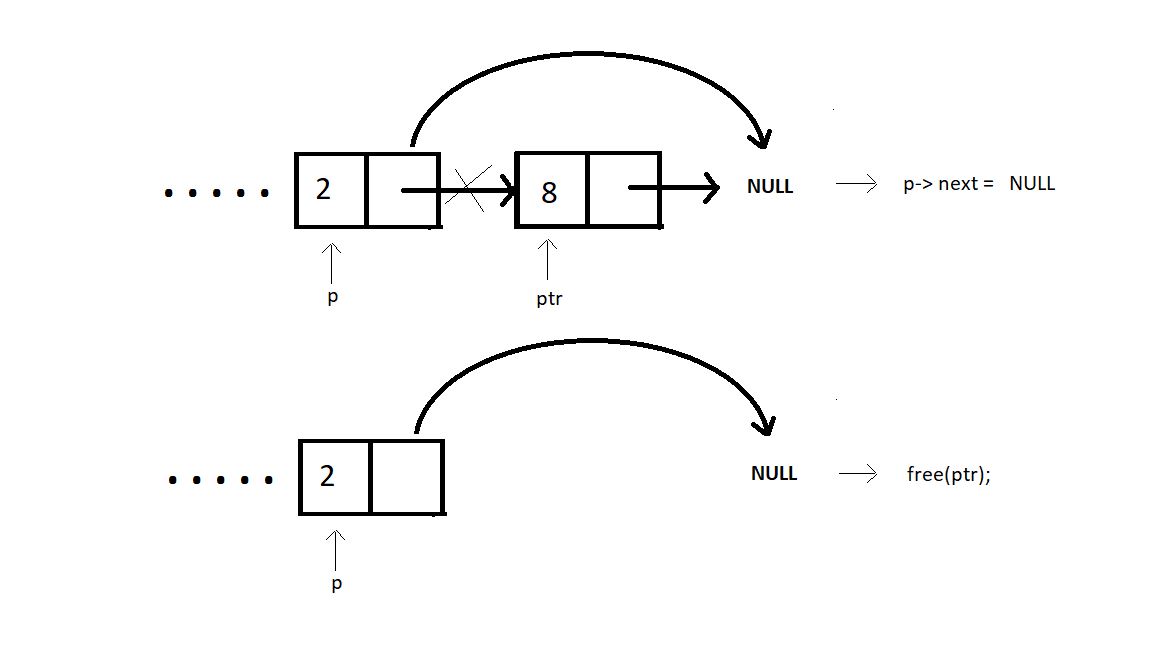
struct Node * deleteAtLast(struct Node * head){
struct Node *p = head;
struct Node *q = head->next;
while(q->next !=NULL)
{
p = p->next;
q = q->next;
}

p->next = NULL;
free(q);
return head;
}

Deleting a node with a given value.

Similar to the other cases, ptr can be deleted for a given value as well by following few steps:
p→next=givenValue→next;
free(givenVal);
Since, the value 8 comes twice in the list, this function will be made to delete only the first occurence.

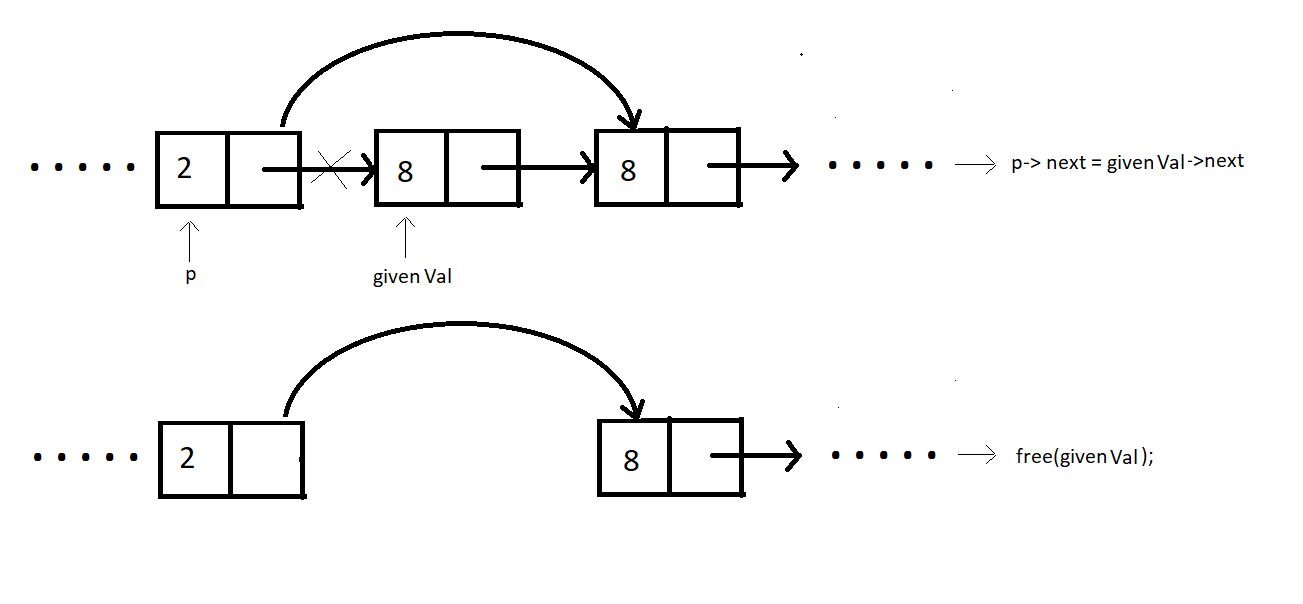
struct Node * deleteByValue(struct Node * head, int value){
struct Node *p = head;
struct Node *q = head->next;
while(q->data!=value && q->next!= NULL)
{
p = p->next;
q = q->next;
}

if(q->data == value){
p->next = q->next;
free(q);
}
return head;
}