Best Case, Worst Case and Average Case Analysis of an Algorithm

Analysis of a search algorithm:

Consider an array that is sorted in increasing order.
1 7 18 50 180
We have to search a given number in this array and report whether it's present in the array or not. In this case, we have two algrotithms, and we will be interested in analyzing their performance separately.

Algorithm 1 - Start from the first element until an element greater than or equal to the number to sbe searched is found.
Algorithm 2 - Check whether the first or the last element is equal to the number. If not, find the number between these two elements (center of the array); if the center element is greater than the number to be searched, repeat the process for the first half else, repeat for the second half until the number is found. And this way, keep dividing your search space, making it faster to search.

Analyzing Algorithm 1: (Linear Search)

We might get lucky enough to find our element to be the first element of the array. Therefore, we only made one comparison which is obviously constant for any size of the array.

Best case complexity = O(1)

If we are not hte afortunate, the element we are searching for might be the last one. Therefore, our program made 'n' comparisions.

Worst case complexity = O(n)

For calculating the average case time, we sum the list of all the possible case's runtime and divide it with the toatal number of cases. Here, we found it to be just O(n). (Sometimes, calculation of average-case time gets very complicated.)

Analyzing Algorithm 2:

If we get really lucky, the first element will be the only element that gets comparedd. Hence, a constatnt time.

Best case comlexity = O(1)

If we get unlucky, we will have to keep dividing the array into halves until we get a single element. (that is, the array gets finished)

Hence the time taken : n + n/2 + n/4 + ..... +1 = logn with base 2

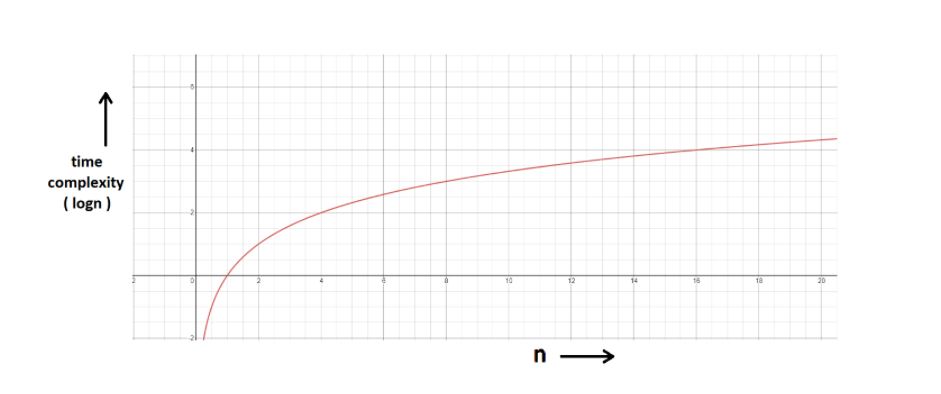
Worst case complexity = O(log n)

What is log(n)?

Logn refers to how many times I need to divide n units until they can no longer ve divided (into halves).

log8 = 3 → 8/2 + 4/3 + 2/2 → can't break anymore
Log 4 = 2 → 4/2 + 2/2 → can't break anymore.

You can refer to the graph below, and you will find how slowly the time complexity (y-axis) increases when we increase the input n (X-axis).

Space complexity