Types of Binary Tree

There are two types of data
- Linear → Arrays, queues, stacks and linked list
- Non-linear → Binary Tree
  - Trees are ideally used to represent hierarchical data
  - Trees are useful in representing an organizational hierarchy.
    Example ↓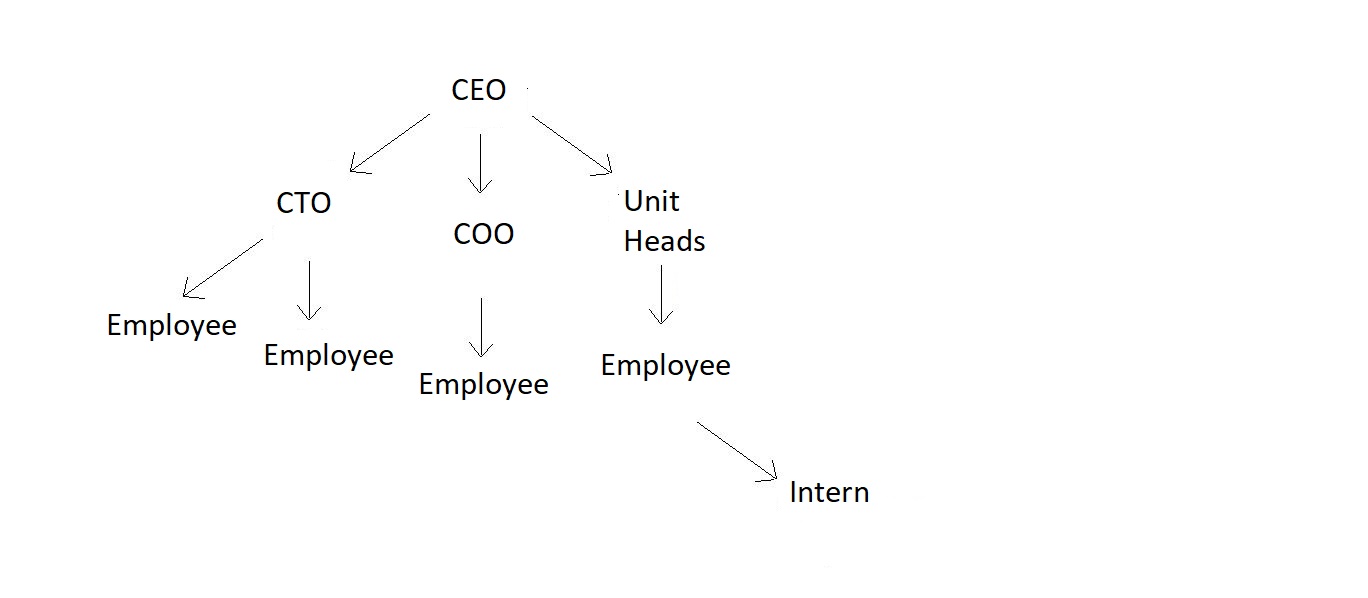
  - Another good example would be our file manager in desktops.
    There is a C Drive, it contains folders Windows, Program Files, etc. Which further contain folders. So, they are hierarchically represented using a tree.

Various types of binary tree

1 → Full or Strict Binary trees:

Strict binary tree is having all of its nodes with a degree of 2 or 0. That is each of its nodes either have 2 children or a leaf node.
Simple example ↓

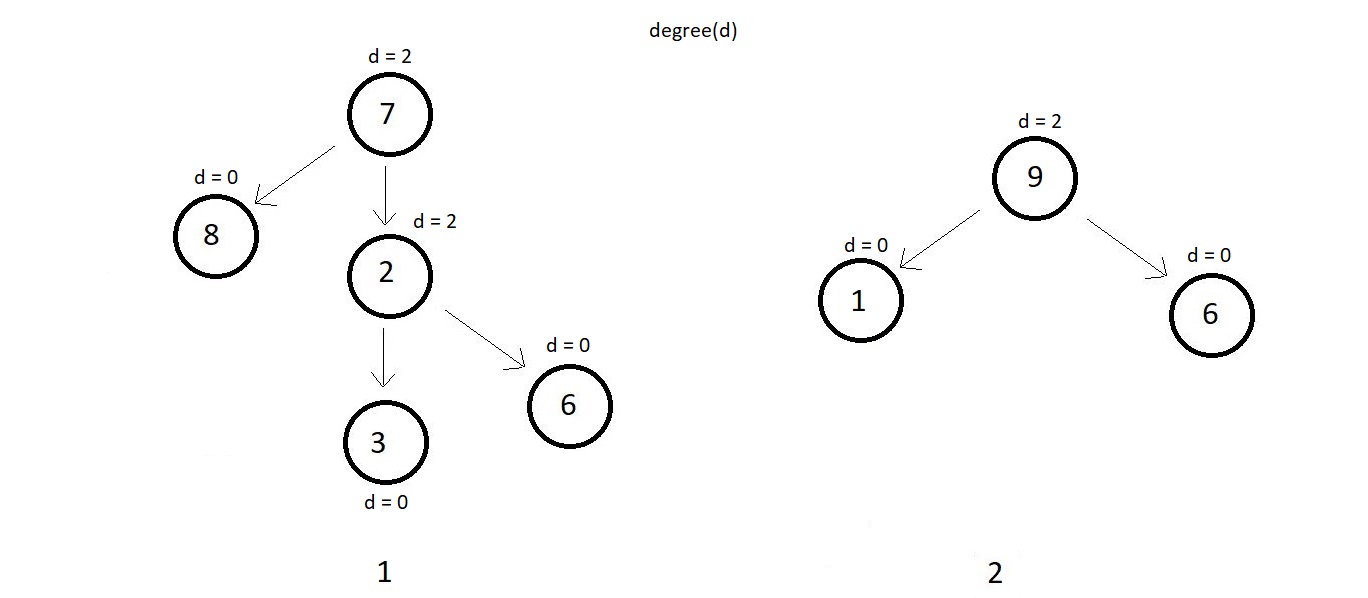
Bellow illustrated is a binary which is not a strict or full binary tree because the colored node has a degree of just 1.

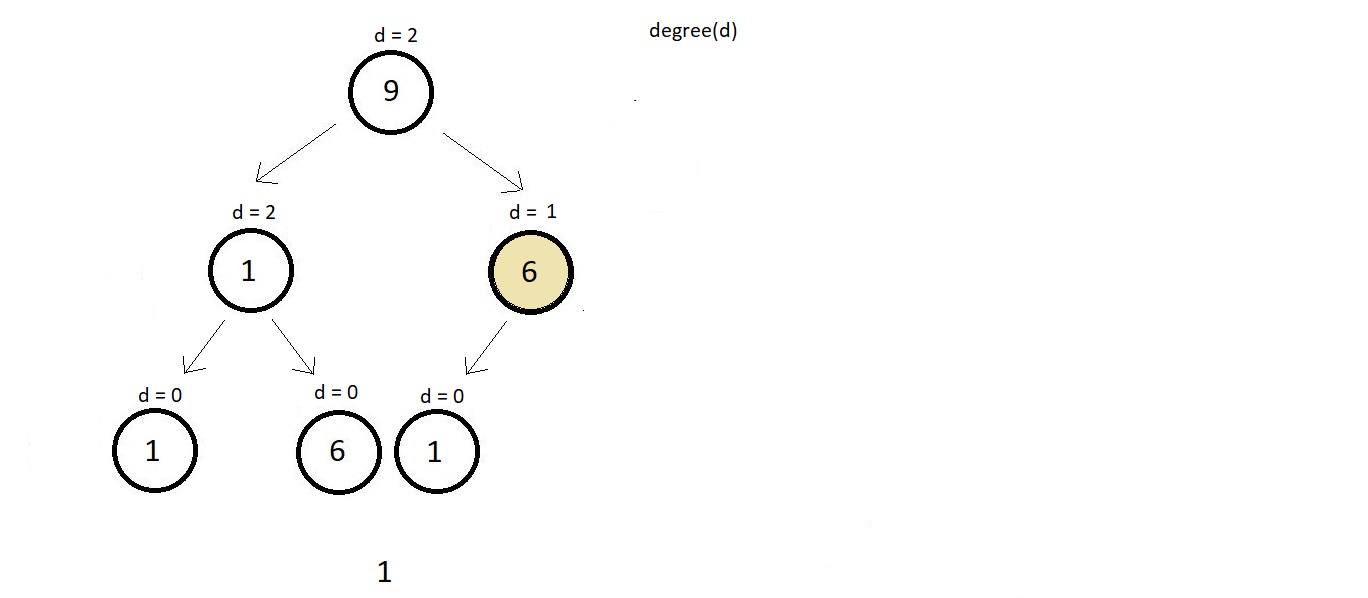
2 → Perfect Binary Tree

A perfect binary tree has all its internal nodes with degree strictly 2 and has all its leaf nodes on the same level. A perfect binary tree as the name suggests appears exaclty perfect. Few examples below.

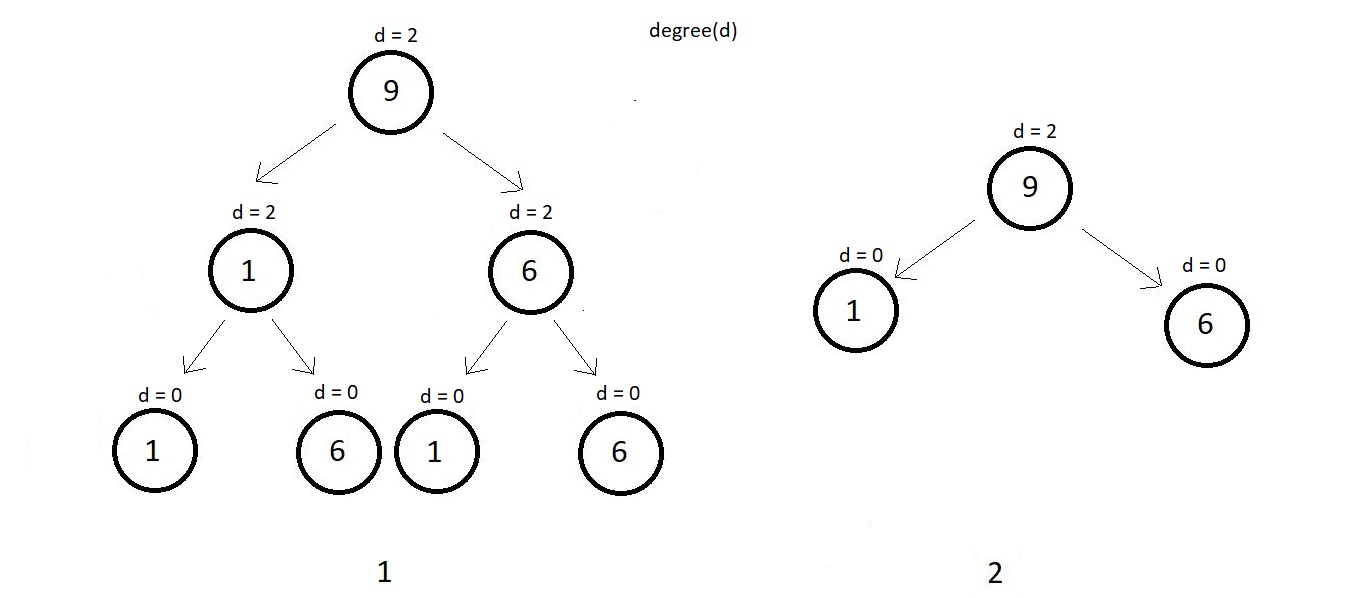
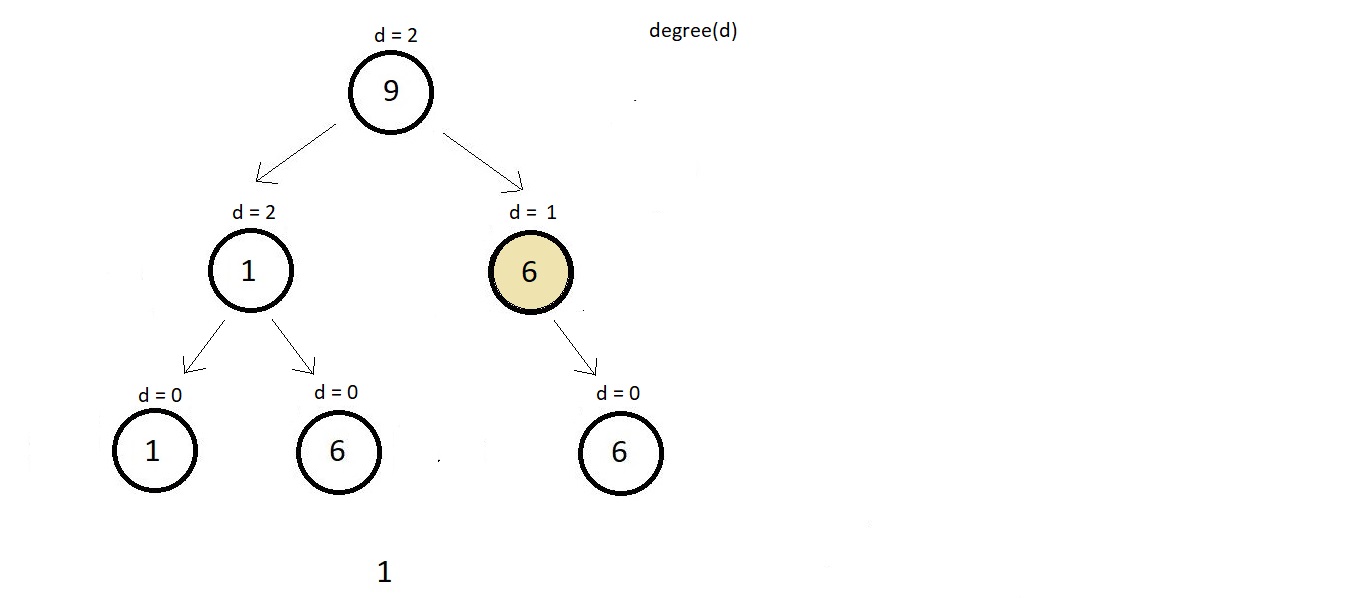
Every leaf node above in both the examples are on the same level and all the internal nodes have a degree 2. Below illustrated is a binary which is not a perfect binary tree because the colored node is an internal node and has a degree of just 1, although each leaf node is on the same leve.

3 → Complete Binary Tree

It has all its levels completely filled except possibly the last level.
And if the last level is not completely filled then the last level's key must be all left-aligned.

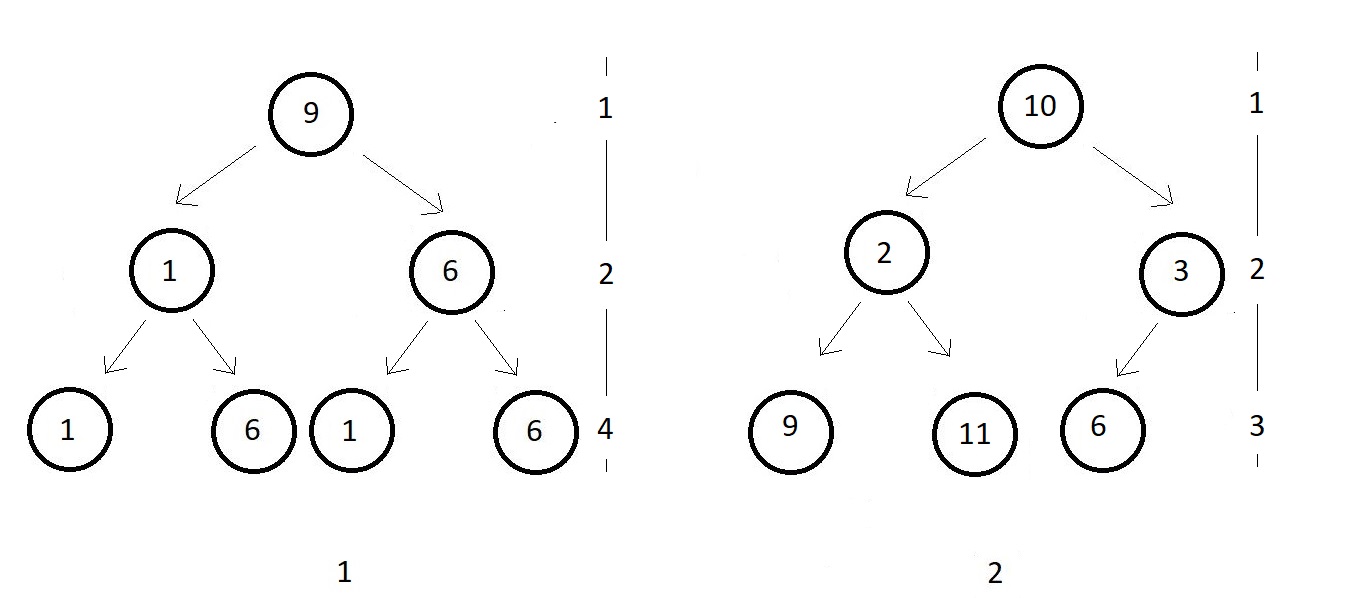
In above figure 1, all levels are completely filled, so nothing further needs to be done. It is a complete binary tree
In figure 2, all nodes are completely filled except the last level which has just 3 keys. It is nonetheless a complete binary tree as all the keys are left-aligned.

Below illustrated are some non-complete binary trees

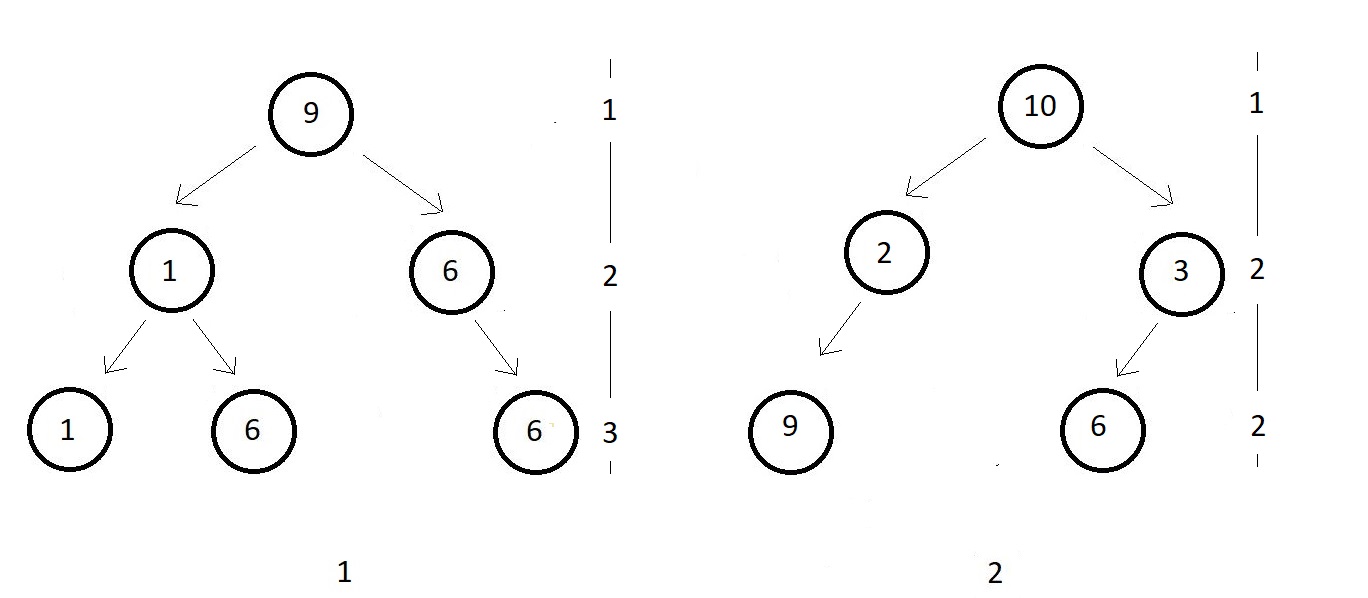
In both the figures, the last level is not complete. And hence we check if all the nodes are algined to the left. But they aren't in both cases. And hence both of them are not complete.

4 → Degenerate tree:

Binary trees where every parent node has just one child and that can be either to its left or right.

Few examples below

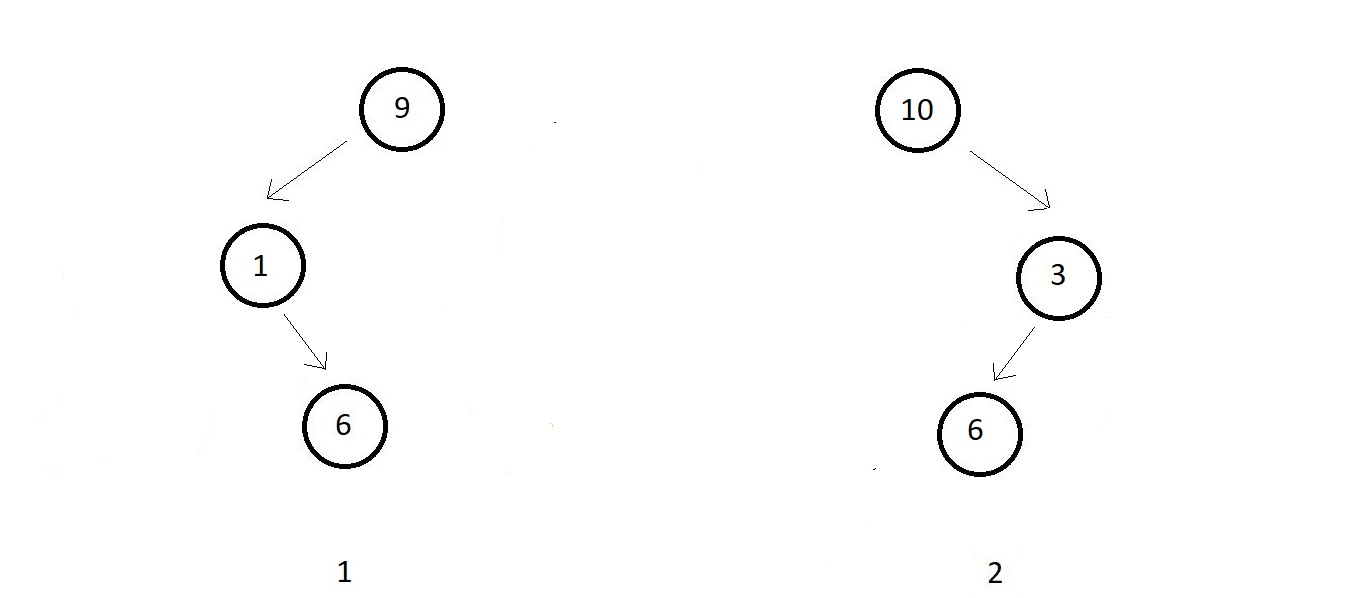
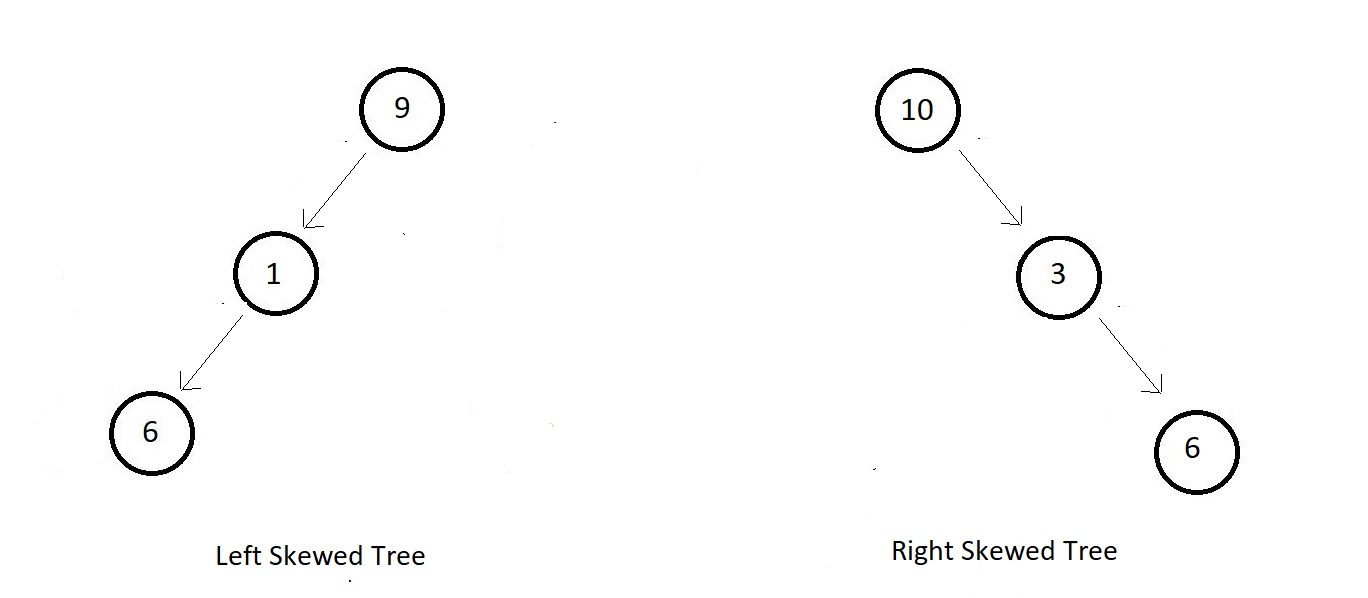
5 → Skewed tree

Binary trees where every parent node has just a single child and that child should ne strict to the left or to the right for all the parents.
- Skewed trees having all the child nodes alighned to the left are called left-skewed trees
- And skewed trees having all the child nodes alighned to the right are called right-skewed trees.
- Example of both left and right-skewed trees