Recursion
Recursive Function : Recursive functions or Recursion is a process when a function calls a copy of
itself to work on smaller problems.
Recursion is the process in which a function calls itself directly or indirectly. And the
corresponding function or function which calls itself is called as recursive function.
- Any function which calls itself is called recursive function.
- This makes life of programmer easy by dividing complex problem into simple or easier problems.
- A termination condition is imposed on such functions to stop them executing copies of themselves forever or infinitely.
- Any problem which can be solved recursively can also be solved iteratively.
- Recursions are used to solve tower of Hanoi, Fibonacci series, factorial finding etc.
Intuitive Understanding
Prepare(Masala Dosa) → prepare(aloo) + prepare(dosa) + prepare(sambhar chutney) ...
Now prepare(aloo) is also going to be divided into small functions
prepare(aloo) → prepare(raw allo)+ prepare(masala)
Now prepare(masala) is a base condition, means it cannot further be divided and it will simply
return a value
Base condition in recursion :
The case at which the function doesn't recur is called the base case.
Recursive case
The instances where the function keeps calling itself to perform a subtask i.e. solving problem by dividing it in small parts, is called the recursive case.
Why Recursions?
- Any problem that can be solved recursively, can also be solved interatively(using loops)
- However, some problems are best suited to be solved using recursion.
- For example, tower of Hanoi, Fibonnaci series, factorial finding, etc.
Example 1: Factorial Calculation
n! = n x n-1 x n-2 x n-3 ......1 also 0! = 1 and 1! = 1 and n!= n x (n-1)!
For factorial Calculation the base case occurs at the parameter value of 0 and 1 (because
they cannot be futher factorized).
#include <stdio.h>
int factorial(int number)
{
if (number == 1 || number == 0)
{
return 1;
}
else
{
return (number * factorial(number - 1));
}
}
int main()
{
int num;
printf("Enter the number you wan the factorial of :");
scanf("%d",&num);
printf("The factorial of %d is %d \n", num , factorial(num));
return 0;
}
Summary : So Recursion is a process in which any function keeps calling itself till any termination
condition is satisfied and in simple words you can think Recursions as same like iteration because
in both of them repetition occurs till any condition
is satisfied or becomes false.
And the most important thing during using recursions is it's
termination condition because most of time the condition given in recursive function is wrong and
because of that
the function is executed infinitely or for forever
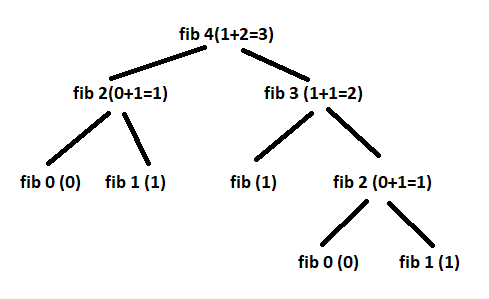
Whey was recursive approach slow?
This topic comes after solving the fibonacci series exercise
Iterative approach takes less time as in case of Fibonacci Series it doesn't call same no. again and again but in Recursive approach it calls same no. again and again i.e. many times.
Recursion tree
In a nut shell...
- Recursions is a good appraoch when it comes to problem solving
- However, programmer needs to evaluate the need and impact of using recurisve/iterative approach while solving a particular problem
- In case of factorial calculation, recursion saved a lot of lines of code.
- However in case of Fibonacci series, recursion resulted in some extra unnecessary function calls which was an extra overhead!
- Running time for Fibonacci series grows exponentially with input in case of recursive approach!