Data Representation
- Digital computers store and process information in binary form as digital logic has only two values "1" and "0" or in other words "True or False".
- This system is called radix 2.
- We human generally deal with radix 10 i.e. decimal.
- As matter of convenience there are many other representations like Octal (Radix 8), Hexadecimal (Radix 16), Binary coded decimal (BCD), Decimal etc.
- Every computer's CPU has a width measured in terms of bits such as 8 bit CPU, 16 bit CPU, 32 bit CPU etc.
- Similarly, each memory location can store a fixed number of bits and is called memory width.
- Given the size of the CPU and Memory, it is for the programmer to handle his data representation.
Data Representation in Computers
- Information handled by a computer is classified as intruction and data.
- A broad overview of the internal representation of the information ↓
- No matter whether data is in numeric or non-numeric form or integer, everything is internally represented in Binary.
- It is up to the programmer to handle the interpretation of the binary pattern and this interpretation is called Data Representation
- Choice of Data representation to be used in a computer is decided by
- The number types to be represented (integer, real, signed, unsigned, etc)
- Range of vlaues likely to be represented (maximum and minimum to be represented)
- The precision of the numbers i.e. maximum accuracy of representation (floating point single precesion, double precision etc)
- If non-numeric i.e. character, character representation standard to be chose.
- ASCII, EBCDIC, UTF are examples of character representation standards.
- The hardware support in terms of word width, instruction.
Integer Representation
- The number of bits used in representing the integer also implies the maximum number that can be represented in the system hardware.
- However for the efficiency of storage and operations, one may choose to represent the integer with one Byte, two Bytes, Four bytes or more.
- This space allocation is translated from the definition used by the programmer while defining a variable as integer short or long and the Instruction Set Architecture.
- In addition to the bit length definition for integers, we also have a choice to represent them
as below:
- Unsigned Integer
- A positive number including zero can be represented in this format.
- All the alloted bits are utilised in defining the number.
- So if one is using 8 bits to represent the unsigned integer, the range of values that can be represented is 28 i.e. "0" to "255".
- If 16 bits are used for representing then the range is 216 i.e. "0 to 65535".
- Signed Integer
- In this format negative numbers, zero and positive numbers can be prepresented.
- A sign bit indicates the magnitude direction as positive or negative.
- There are three posibble representations signed integer and these are Sign Magitude format, 1's Compliment format and 2's Compliment format.
- Unsigned Integer
Sign Magnitude Format
- Most Significant Bit (MSB) is reserved for indicating the direction of the magnitude (value).
- A "0" on MSB means a positive number and a "1" on MSB means a negative number.
- If n bits are used for representation, n-1 bits indicate the absolute value of the number.
- Example for n = 8
- 0010 1111 = + 47 Decimal (Positive number)
- 1010 1111 = - 47 Decimal (Negative Number)
- 0111 1110 = +126 (Positive number)
- 1111 1110 = -126 (Negative Number)
- 0000 0000 = + 0 (Postive Number)
- 1000 0000 = - 0 (Negative Number)
- Although this method is easy to understand, Sign Magnitude representation has several
shortcomings like
- Zero can be represented in two ways causing redundancy and confusion.
- The total range for magnitude representation is limited to 2n-1, although n bits were accounted.
- The separate sign bit makes the addition and subtraction more complicated. Also comparing two numbers is not straigt forward.
1's Complement Format
- In this format too, MSB is reserved as the sign bit.
- But the difference is in representing the Magnitude part of the value for negative numbers (magnitude) is inversed and hence called 1's Complement form.
- The positive numbers are represented as it is in binary.
- Examples for n = 8
- 0010 1111 = + 47 Decimal (Positive number)
- 1101 0000 = - 47 Decimal (Negative Number)
- 0111 1110 = +126 (Positive number)
- 1000 0001 = -126 (Negative Number)
- 0000 0000 = + 0 (Postive Number)
- 1111 1111 = - 0 (Negative Number)
notes
Converting a given binary number to its 2's complement form
- Step 1 → -x = x' + 1 where x' is the one's complement of x.
- Step 2 → Extend the data width of the number, fill up with sign extension i.e. MSB bit is used to fill the bits.
- Example : -47 decimal over 8bit representation
- Binary equivalent of + 47 is 0010 1111
- Binary equivalent of - 47 is 1010 1111 (Sign Magnitude Form)
- 1's complement equivalent is 1101 0000
- 2’s complement equivalent is 1101 0001
- As you can see zero is not getting represented with redundance.
- There is only one way of representing zero.
- The other problem of the comlexity of the arithmetic operation is also eliminated in 2's complement representation.
- Subraction is done as Addition.
Floating Point Number System
more notes- The maximum number at best represented as a whole number is 2n.
- In Scientific world, we do come across numbers like Mass of an Electron is 9.10939 x 10-31 Kg. Velocity of light is 2.99792458 x 108 m/s.
- It makes no sense to write a number in non-readable form or non-processible form.
- Hence we write such large or small numbers using exponent and mantissa.
- This is said to be Floating Point representation or real number representation.
- Representationin computer
- Unlike the two's compliment representation for integer numbers, Floating Point number uses Sign and Magnitude representation for both mantissa and exponent,
- In the number 9.10939 x 10-31, in decimal form, -31 is Exponent, 9.10939 is known as Fraction. Mantissa, Significand and fraction are synonymously used terms.
Floating Point Representation
- We have two standard known as Single Precision and Double Precision from IEEE.
- These standards enable portability among different computers.
- Single Precision uses 32bit format.
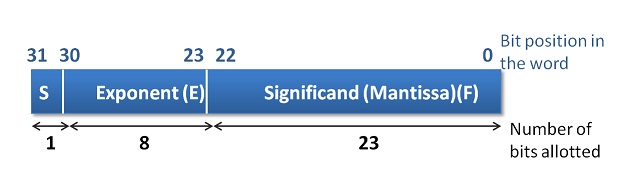
- Single Precision can represent exponent in the range -127 to +127.
- It is possible as a result of arithmetic operations the resultinf exponent may not fit in. This situation is called overflow in case of positive exponent and underflow in the case of negative exponent.

- Double precision can represent fractions with larger accuracy.
- The Double Precision format has 11 bits for exponent meaning a number as large as -1023 to 1023 can be represented.
- Generally, a special purpose CPU known as Co-processor is used.
- This Co-processor works in tandem with the main CPU.
- The programmer shoulb be using the float declaration only if his data is in real number form. float declaration is not to be used generously.
