Advanced Encrption Algorithm
Advanced Encryption Algorithms (AEA) are sophisticated techniques used to secure data and ensure confidentiality in modern cryptographic systems. These algorithms are designed to provide robust protection against unauthorized access by leveraging complex mathematical operations. This unit explores some of the widely used encryption algorithms, such as Blowfish, International Data Encryption Algorithm (IDEA), and RC-5, along with their unique features and applications. Additionally, it delves into key concepts like Symmetric Key Distribution, which facilitates secure key sharing, and Random Number Generators, critical for generating unpredictable keys. Lastly, the Placement of the Encryption Function is examined, highlighting its significance in optimizing security and system performance.
Blowfish Algorithm
- Blowfish is a block cipher encryption algorithm.
- It follows symmetric key cryptography, where the same key is used for both encryption and decryption.
- Input size (block size) is fixed at 64 bits.
- The key size is variable, ranging from 32 to 448 bits.
Properties
- Fast encryption and decryption process, making it suitable for real-time applications.
- Requires less memory, making it efficient for resource-constrained environments.
- Simple to understand and implement compared to other complex encryption algorithms.
- Highly secure due to the use of a variable-length key, allowing for flexibility in security strength.
- Resistant to known cryptographic attacks like brute force due to its key size flexibility.
Blowfish Algorithm Steps
The Blowfish algorithm consists of two main steps:
- Key Generation: Generates subkeys and initializes the algorithm components.
- Data Encryption: Encrypts plaintext using the generated keys and the block cipher process.
Key Generation
-
Keys are stored in an array:
- Array elements: k1, k2, k3, ..., kn where 1 ≤ n ≤ 14.
- Each key block has a length of 32 bits.
- The total key length can be up to 448 bits (32 × 14), which is a multiple of 32.
-
Initialize the P-array:
- The P-array consists of 18 subkeys: P1, P2, P3, ..., P18.
- Each element in the P-array is 32 bits long.
-
Initialize the S-boxes:
- There are 4 S-boxes, each containing 256 entries.
-
Example for S-box initialization:
- S1: s0, s1, ..., s255
- S2: s0, s1, ..., s255
- The same pattern applies for S3 and S4.
- Initialize each element of the P-array and S-boxes with predefined hexadecimal values.
-
Perform XOR operations to further initialize the P-array:
- P1 = P1 XOR K1
- P2 = P2 XOR K2
- ... (continue for all key values)
- When all 14 keys are used, restart from K1 for the remaining P-array elements.
-
Example:
- P15 = P15 XOR K1
- P18 = P18 XOR K4
-
Process a 64-bit block of plaintext (initially all bits are 0) to generate subkeys:
- Initial plaintext: (0, 0, 0, ..., 0)
- Subkeys are generated and used in the encryption process.
Data Encryption
-
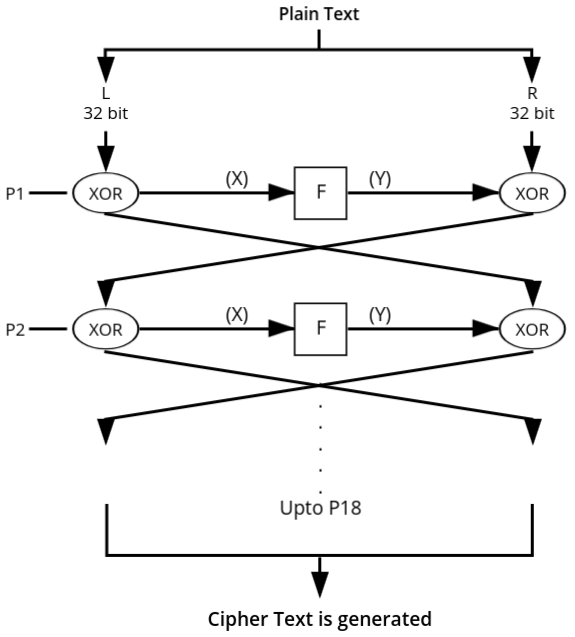
The plaintext size is 64 bits, which is divided into two halves:
- The left half (L) consists of the first 32 bits.
- The right half (R) consists of the remaining 32 bits.
-
The encryption process involves the following steps:
- The left half (L) is XORed with the first subkey (P1).
- The result of this XOR operation (denoted as `x`) is input to the function `F` to produce an output (denoted as `y`).
- The output `y` is XORed with the right half (R).
- After XORing, the left and right halves are swapped.
- This process is repeated for all 18 subkeys in the P-array (P1 to P18).
-
After processing through all 18 rounds:
- The final left (L) and right (R) halves are combined to form a 64-bit block of ciphertext.
- The swapping step ensures the encryption provides strong diffusion and security.
Understanding the Function (F)
-
The input to the function `F` is 32 bits, which is divided into four 8-bit segments:
- Each 8-bit segment is independently processed by one of the four S-boxes (S1, S2, S3, S4).
-
The output of the S-boxes undergoes the following operations:
- The output of S-box 1 is XORed with the output of S-box 2.
- The result of this XOR operation is then XORed with the output of S-box 3.
- Finally, the result is XORed with the output of S-box 4.
- The final output of the function `F` is a 32-bit value (denoted as `y`), which is used in the encryption process.
- The purpose of the function `F` is to provide a non-linear transformation of the input, contributing to the algorithm's security by introducing confusion and diffusion.
IDEA Algorithm (International Data Encryption Algorithm)
- It is a block cipher algorithm.
- It follows symmetric key cryptography.
- Uses a Feistel structure for its operations.
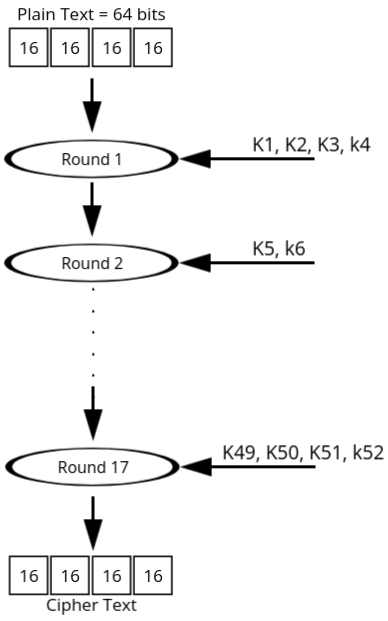
- The input plaintext size is 64 bits, divided into four 16-bit blocks.
- The key size is 128 bits, which is expanded into 52 subkeys.
- Number of rounds = 17 (16 primary rounds + 1 final transformation round).
- Odd-numbered rounds use 4 keys, while even-numbered rounds use only 2 keys.
- The goal of each round is to scramble and mix the data so much that it becomes completely unrecognizable by the end.
Working
- The plaintext of 64 bits is divided into 4 equal parts, each of size 16 bits.
- These 4 parts are denoted as X1, X2, X3, and X4.
- The algorithm involves 17 rounds, out of which 16 are primary rounds and the 17th is a final transformation round.
- Each round processes the input blocks using specific subkeys from the 52 subkeys generated during the key expansion phase.
- For each round:
- Subkeys are applied to the blocks using modular addition, modular multiplication, and XOR operations.
- Data blocks are mixed to ensure confusion and diffusion.
- Odd and even rounds have distinct operations, explained further below.
- The final transformation round applies the last 4 subkeys (K49, K50, K51, K52) to the blocks.
- After all rounds, the 4 resulting 16-bit blocks are concatenated to form the 64-bit ciphertext.
What Happens in Each Round?
Each round involves processing the 4 parts (X1, X2, X3, X4) using subkeys and simple operations to create layers of scrambling. Here's how it works:
Odd Rounds (e.g., Round 1, 3, 5...):
- 4 subkeys are used, one for each part: X1, X2, X3, and X4.
- The keys are applied directly to the parts, followed by rearrangements and combinations to mix the data.
- The result is passed to the next round.
Even Rounds (e.g., Round 2, 4, 6...):
- 2 subkeys are used instead of 4, making these rounds slightly different from the odd rounds.
- The keys are applied to specific parts of the data, followed by scrambling and rearrangements.
- This adds another layer of complexity to the scrambled data.
Final Round (Round 17):
- The 4 parts (X1, X2, X3, X4) are processed with the last set of subkeys.
- This step finalizes the ciphertext.
- The scrambled 4 parts are combined into the final 64-bit ciphertext.
RC5 Algorithm (Rivest Cipher)
- A symmetric key block cipher encryption algorithm.
- Processes two-word blocks at a time; the plaintext is divided into two equal-sized blocks.
- It has three main parameters:
- w: Word size (16, 32, or 64 bits).
- r: Number of rounds (can range from 0 to 255).
- b: Key size in bits (ranges from 0 to 255).
These parameters are chosen based on the requirements of the input plaintext.
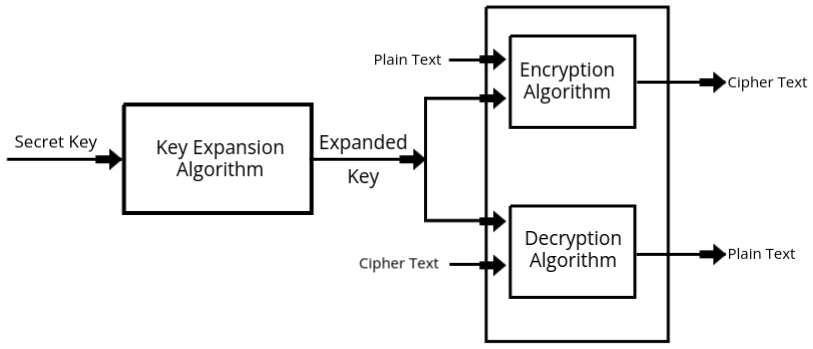
- The algorithm consists of three main components:
- Key Expansion: Expands the secret key into a series of subkeys.
- Encryption: Transforms plaintext into ciphertext using subkeys.
- Decryption: Reverses the encryption process to retrieve the original plaintext.
Block Diagram
- The secret key is first processed through the Key Expansion Algorithm to generate multiple subkeys. For example, a 128-bit secret key can be expanded into a sequence of subkeys depending on the block size.
- These subkeys are then used during the encryption rounds to transform the plaintext into ciphertext.
- During decryption, the same subkeys are used in reverse order to retrieve the original plaintext.
What Happens in Each Stage?
1. Key Expansion
- Key expansion is a preprocessing step that generates a large number of subkeys from the original secret key.
Steps:
- The plaintext of 64 bits is divided into two equal blocks: A (32 bits) and B (32 bits).
- The secret key is expanded into a subkey array S, containing 2(r+1) subkeys (e.g., S[0], S[1], ..., S[2r+1]).
- Initial values for A and B are created by adding the first two subkeys:
- A = A + S[0]
- B = B + S[1]
2. Encryption
- Encryption involves multiple rounds of transformations using subkeys.
- Each round performs the following steps:
- A is updated using a combination of bitwise operations (XOR, left rotation) and addition with a subkey.
- B is updated in a similar manner using the next subkey.
- After completing all rounds, the output is combined to form the final ciphertext.
3. Decryption
- The decryption process reverses the encryption steps.
- It uses the same subkeys, but applies them in reverse order.
- By undoing the operations (e.g., subtracting instead of adding, reversing rotations), the ciphertext is converted back into the original plaintext.
Symmetric Key Distribution
- Symmetric key cryptography requires both sender and receiver to use the same secret key for encryption and decryption.
- The major challenge lies in securely sharing this secret key between the communicating parties.
- Several methods exist for key distribution, each with its own advantages and drawbacks.
Methods of Symmetric Key Distribution
1. Pre-Shared Key
- The secret key is manually shared between the sender and receiver before communication begins.
- This can be done using secure channels such as:
- Face-to-face meetings.
- Delivery by trusted couriers.
- Advantages:
- Simple and direct for small-scale systems.
- Does not require additional infrastructure.
- Drawbacks:
- Not practical for large-scale or geographically distributed systems.
- Risk of key interception during transmission.
2. Using a Trusted Third Party (Key Distribution Center)
- A trusted third party, called a Key Distribution Center (KDC), facilitates the secure exchange of keys.
- Steps:
- The sender and receiver each establish a secure connection with the KDC.
- The KDC generates a unique session key for communication between the two parties.
- This session key is securely transmitted to both parties by the KDC.
- Advantages:
- Eliminates the need for direct key sharing between sender and receiver.
- Scalable for larger systems.
- Drawbacks:
- The KDC becomes a single point of failure.
- Requires additional infrastructure and trust in the KDC.
3. Using Symmetric Encryption with Public Key Infrastructure (PKI)
- Public key cryptography is used to securely exchange symmetric keys.
- Steps:
- The sender encrypts the symmetric key with the receiver's public key.
- The encrypted key is transmitted to the receiver.
- The receiver decrypts the key using their private key.
- Advantages:
- Secure even over insecure channels.
- Scalable for large systems.
- Drawbacks:
- Requires a functioning PKI infrastructure.
- Introduces additional computational overhead.
4. Diffie-Hellman Key Exchange
- A mathematical algorithm allows two parties to generate a shared symmetric key over an insecure channel.
- Steps:
- Both parties agree on a public base and a public modulus.
- Each party selects a private key and generates a public value using the agreed parameters.
- They exchange public values and compute the shared secret key using their private key.
- Advantages:
- Secure key generation over insecure channels.
- No prior shared secret is required.
- Drawbacks:
- Vulnerable to man-in-the-middle attacks if authentication is not used.
- Limited to key agreement, not encryption itself.
Challenges in Symmetric Key Distribution
- Ensuring secure key transfer without interception.
- Managing keys in systems with a large number of users.
- Handling key revocation and replacement in case of compromise.
Random Number Generators in Cryptography
- Random numbers are crucial in cryptography for tasks like key generation, nonce creation, and secure communication.
- They ensure unpredictability, making cryptographic algorithms secure against attacks.
- There are two main types of random number generators:
- True Random Number Generators (TRNGs)
- Pseudo-Random Number Generators (PRNGs)
Types of Random Number Generators
1. True Random Number Generators (TRNGs)
- Generate randomness based on physical phenomena such as:
- Thermal noise.
- Electromagnetic interference.
- Radioactive decay.
- Features:
- Non-deterministic: Results cannot be predicted.
- Highly secure for cryptographic applications.
- Drawbacks:
- Slower than PRNGs due to dependency on physical events.
- Requires specialized hardware to collect randomness.
2. Pseudo-Random Number Generators (PRNGs)
- Generate randomness using mathematical algorithms based on a seed value.
- Features:
- Deterministic: Output depends on the seed, making it reproducible if the seed is known.
- Faster than TRNGs and suitable for software implementations.
- Drawbacks:
- Less secure if the seed or algorithm is compromised.
- Not truly random, as the randomness relies on the algorithm's complexity.
Cryptographically Secure PRNGs (CSPRNGs)
- A special class of PRNGs designed for cryptographic applications.
- Features:
- Passes stringent randomness tests, ensuring unpredictability.
- Resilient against attacks, even if part of the output is known.
- Examples:
- Yarrow Algorithm.
- Fortuna Algorithm.
- Dual_EC_DRBG (now deprecated due to vulnerabilities).
Applications in Cryptography
- Key Generation: Random numbers are used to generate cryptographic keys that are unpredictable.
- Initialization Vectors (IVs): Randomness ensures that IVs are unique for each encryption operation.
- Nonces: Unique random values prevent replay attacks in protocols.
- Salt Values: Random salts ensure secure password hashing by preventing rainbow table attacks.
Challenges in Random Number Generation
- Bias: Random numbers must be uniformly distributed without any bias.
- Predictability: Ensuring unpredictability is critical, especially for PRNGs.
- Entropy Source: TRNGs rely on sufficient entropy from physical phenomena, which can be limited.