Public Key Encryption
Public Key Encryption, also known as Asymmetric Key Cryptography, is a foundational concept in modern cryptography that enables secure communication over insecure channels. Unlike Symmetric Key Cryptography, where the same key is used for both encryption and decryption, Public Key Encryption uses a pair of keys: a public key (used for encryption) and a private key (used for decryption). This revolutionary concept has made it possible for individuals and organizations to securely exchange sensitive information without the need for a pre-shared secret key, making it an essential tool for secure online transactions, email encryption, and digital signatures.
This topic is divided into several critical areas, each building upon the concept of public key encryption and its various applications:
- Difference Between Symmetric and Asymmetric Key Cryptosystems: This section explores the fundamental differences between symmetric (or secret-key) cryptosystems and asymmetric (or public-key) cryptosystems. Symmetric systems use a single key for both encryption and decryption, which requires secure key exchange mechanisms. In contrast, asymmetric systems solve this problem by using two keys: a public key, which can be freely shared, and a private key, which remains confidential. Understanding these differences is crucial for grasping the strengths and limitations of each approach in real-world cryptographic applications.
- Public-Key Cryptography: The heart of the topic, public-key cryptography, encompasses the principles
that underpin asymmetric encryption systems. Public-key systems rely on the mathematical properties of
numbers and their operations to create secure systems. This section covers key cryptosystems used in
real-world applications:
- Principles of Public-Key Cryptosystems: These are the core concepts that explain how asymmetric encryption works, including how public and private keys interact, and the role of mathematical functions in providing security.
- RSA Algorithm: One of the most widely used public-key cryptosystems, RSA relies on the difficulty of factoring large prime numbers. It is the basis for securing web traffic (e.g., SSL/TLS), digital signatures, and more.
- Rabin Cryptosystem: A less well-known but important cryptosystem, Rabin's method is based on the difficulty of extracting square roots modulo large primes, and its security parallels RSA in some ways.
- ElGamal Cryptosystem: Another key public-key cryptosystem, ElGamal is based on the Diffie-Hellman key exchange and provides both encryption and digital signatures.
- Key Management: Key management refers to the processes and techniques involved in creating, distributing, storing, and updating cryptographic keys in a secure manner. Proper key management is crucial for maintaining the security of a cryptographic system, as the security of encrypted data is only as strong as the protection of the keys used to encrypt it.
- Public Key Distribution: Public key distribution deals with the problem of securely sharing public keys across an insecure network. Even though the public key is not secret, it must be delivered in such a way that an attacker cannot substitute a fake key. Various methods, such as certificates issued by a trusted Certificate Authority (CA), are used to ensure that the recipient is truly receiving the intended public key.
- Mathematical Foundations: The security of public-key cryptosystems is deeply rooted in number theory,
particularly in the use of certain mathematical theorems that make encryption difficult to break:
- Fermat’s Theorem: Fermat's Little Theorem provides the basis for many public-key algorithms, such as RSA, by asserting properties of numbers in modular arithmetic, particularly in prime number fields.
- Euler’s Theorem: This theorem extends Fermat’s work and is used in algorithms like RSA for key generation, ensuring that decryption works correctly by defining the relationship between the totient of a number and modular exponentiation.
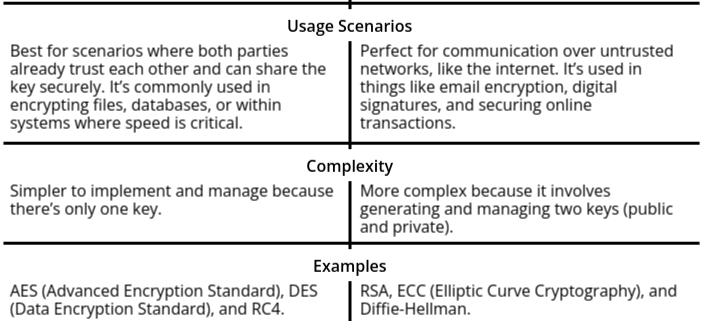
Difference Between Symmetric and Asymmetric Key Cryptosystems
- We know that Cryptography is all about keeping information safe and secure. Suppose you want to send a secret message to your friend without anyone else being able to read it. This is where cryptosystems come in. A cryptosystem is basically a framework or a set of rules, tools, and techniques used to protect information. It includes methods to encrypt (convert readable data into an unreadable format) and decrypt (turn the unreadable format back into readable data) messages. At the heart of every cryptosystem are keys, which act as the "special codes" that lock and unlock this information.
- Now, there are two main types of cryptosystems based on how these keys are used: symmetric key cryptosystems and asymmetric key cryptosystems. Both are like tools in a toolkit designed to solve the same problem keeping data secure but they work in very different ways.
- A symmetric key cryptosystem is the simpler of the two. It’s like sharing the same key to lock and unlock a box. Both you and your friend have the exact same key, which you use to encrypt (lock) and decrypt (unlock) messages. This method is straightforward and fast, making it ideal for situations where speed is critical, like encrypting files or databases. However, there’s a catch: you need to ensure the key remains secret. If anyone else gets their hands on it, they can read all the messages. Plus, securely sharing the key with someone else can be tricky, especially if they’re far away.
- On the other hand, an asymmetric key cryptosystem is a bit more advanced. It uses two keys: a public key and a private key. Think of it like a mailbox. The public key is like the slot where anyone can drop letters (encrypt messages), but only you, with your private key, can open the mailbox and read those letters (decrypt them). This makes it perfect for secure communication over the internet, where you don’t have to worry about someone intercepting the key. Even if someone knows your public key, they can’t use it to decrypt messages because they don’t have the matching private key.
- So, in summary, cryptosystems are the backbone of secure communication. Symmetric systems are fast and efficient but rely on keeping one key secret, while asymmetric systems are slower but far more secure, especially for sharing information over untrusted networks. Each has its strengths, and they are often used together to create a robust and secure system.

Understanding the RSA Algorithm
The RSA algorithm is a cornerstone of modern cryptography. It’s widely used to ensure secure communication, especially over the internet. Named after its inventors—Ron Rivest, Adi Shamir, and Leonard Adleman—it is a method of asymmetric encryption. Unlike symmetric systems where one key is shared between the sender and receiver, RSA works with two keys: a public key and a private key. This separation of keys adds an extra layer of security and makes RSA one of the most trusted encryption methods in use today.
What is the RSA Algorithm?
- RSA is a cryptographic algorithm that uses the mathematical properties of prime numbers to secure information.
- It relies on two keys:
- Public Key: Used to encrypt messages and shared openly.
- Private Key: Used to decrypt messages and kept secret by the owner.
- The security of RSA lies in the difficulty of prime factorization, making it extremely hard to reverse-engineer the original primes used to generate the keys.
How Does RSA Work?
To understand RSA, let’s break it into three main stages: Key Generation, Encryption, and Decryption. Each stage involves some fascinating mathematical principles that make RSA both secure and effective.
1. Key Generation
- Step 1: Choose Two Large Prime Numbers
- Select two large prime numbers \( p \) and \( q \). These primes should be random, unique, and very large (hundreds of digits long for modern security).
- Example: \( p = 61 \), \( q = 53 \).
- Step 2: Compute \( n \)
- Multiply \( p \) and \( q \) to get \( n \): \[ n = p \times q \]
- \( n \) is a part of both the public and private keys. It defines the range of possible values for encryption and decryption.
- Example: \( n = 61 \times 53 = 3233 \).
- Step 3: Compute \( \phi(n) \)
- \( \phi(n) \), called Euler’s Totient Function, is calculated as: \[ \phi(n) = (p - 1) \times (q - 1) \]
- Example: \( \phi(3233) = (61 - 1) \times (53 - 1) = 3120 \).
- Step 4: Choose an Encryption Exponent (\( e \))
- Select a number \( e \) that is relatively prime to \( \phi(n) \), meaning they share no common factors other than 1.
- Common choices for \( e \): 3, 17, or 65537.
- Example: Let \( e = 17 \).
- Step 5: Calculate the Decryption Exponent (\( d \))
- Find \( d \), the modular multiplicative inverse of \( e \) modulo \( \phi(n) \), satisfying: \[ (d \times e) \mod \phi(n) = 1 \]
- Example: \( d = 2753 \).
- Final Output:
- Public Key: \( (e, n) = (17, 3233) \).
- Private Key: \( (d, n) = (2753, 3233) \).
2. Encryption
- Represent the message \( M \) as a number smaller than \( n \). For example, \( A = 1, B = 2, ..., Z = 26 \).
- Encrypt \( M \) using the public key \( (e, n) \): \[ C = M^e \mod n \]
- Example: Let \( M = 65 \). Encrypt: \[ C = 65^{17} \mod 3233 = 2790 \]
- The ciphertext \( C = 2790 \) is sent to the receiver.
3. Decryption
- Use the private key \( (d, n) \) to decrypt the ciphertext \( C \): \[ M = C^d \mod n \]
- Example: Decrypt \( C = 2790 \): \[ M = 2790^{2753} \mod 3233 = 65 \]
- The receiver restores the original message \( M = 65 \).
Strengths and Weaknesses of RSA
- Strengths:
- Provides strong security through its asymmetric key system.
- Compatible with a wide range of systems and use cases.
- Facilitates secure communication without prior key sharing.
- Weaknesses:
- Slower than symmetric encryption algorithms.
- Requires larger key sizes (2048 bits or more) for adequate security.
- Vulnerable to potential quantum computing advancements in the future.
Applications of RSA
- Secure Web Browsing: Used in SSL/TLS for HTTPS.
- Email Encryption: Protects sensitive emails (e.g., PGP).
- Digital Signatures: Verifies the authenticity of documents and software.
- Key Exchange: Helps securely share symmetric keys.
Understanding the Rabin Cryptosystem
The Rabin Cryptosystem is another form of asymmetric encryption. It’s named after its inventor, Michael Rabin, who introduced it in 1979. Like the RSA algorithm, the Rabin Cryptosystem uses public and private keys to ensure secure communication, but the mathematical principles behind it are slightly different.
The Rabin Cryptosystem is based on quadratic residues and the difficulty of factoring large numbers. Its security is grounded in the assumption that it is computationally hard to solve the quadratic residuosity problem, which is believed to be a difficult problem for computers to solve, similar to how RSA depends on the difficulty of factoring large integers.
Let's break it down step by step so you can fully grasp how it works.
What is the Rabin Cryptosystem?
- The Rabin Cryptosystem is an asymmetric encryption algorithm that relies on the mathematical concept of quadratic residues. In simple terms, quadratic residues are numbers that are the result of squaring integers modulo some number.
- The Rabin Cryptosystem works by exploiting the fact that, given a number \(y\), finding its square root modulo a large prime number \(p\) is hard (this is the quadratic residuosity problem).
- The key idea behind Rabin’s system is that it uses modular arithmetic with prime numbers and is somewhat similar to RSA in its key generation process, but it operates differently when it comes to encryption and decryption.
Why is the Rabin Cryptosystem Important?
- Like RSA, the Rabin Cryptosystem enables secure communication over untrusted networks. However, Rabin’s system has a more efficient encryption process because it uses a smaller number of operations to encrypt messages, making it faster in some cases.
- It’s also simpler than RSA in terms of its mathematical operations.
- But, while RSA is widely used for general encryption purposes, the Rabin Cryptosystem has limitations, especially with decryption ambiguity (which we will explain shortly). It’s less commonly used in practice but is an important theoretical system in the study of cryptography.
How Does the Rabin Cryptosystem Work?
- Key Generation: The first step is generating the public and private keys. The
process goes like this:
- Step 1: Choose a large prime \( p \). Select a large prime number \( p \). This number should be large enough (at least 512 bits) to ensure security. Example: \( p = 3233 \).
- Step 2: Calculate the Public Key. The public key in Rabin’s system consists of the prime number \( p \) that you’ve selected. The public key is simply \( p \). Public Key: \( (p) \).
- Step 3: Compute the Private Key. The private key is computed by selecting a number \( x \) that is the square root modulo \( p \). This \( x \) is kept secret. To find \( x \), solve the equation \( x^2 \equiv m \pmod{p} \) for some message \( m \), where \( m \) is a number between 0 and \( p-1 \). This step is mathematically challenging, which is why this system works on the assumption that finding square roots modulo a large prime is computationally difficult. Private Key: \( x \).
- Encryption: Encryption in the Rabin Cryptosystem is done using the public key.
Here’s how encryption works:
- Step 1: Represent the Message. The message to be encrypted, \( m \), is represented as a number. This number should be less than \( p \). Example: Suppose we want to encrypt \( m = 123 \).
- Step 2: Compute the Ciphertext. The ciphertext \( C \) is computed as the square of the message \( m \) modulo \( p \): \[ C = m^2 \mod p \] Example: Suppose \( p = 3233 \) and \( m = 123 \), then the ciphertext is: \[ C = 123^2 \mod 3233 = 15129 \mod 3233 = 2130 \] The ciphertext \( C = 2130 \) is then sent to the receiver.
- Decryption: Decryption is where things get interesting in the Rabin
Cryptosystem. Here’s the tricky part: while encryption is simple, decryption can result in
multiple possible messages because of the properties of squaring numbers.
- Step 1: Use the Private Key to Find the Square Root. The receiver, using their private key, tries to compute the square roots of the ciphertext modulo \( p \). Since squaring is a many-to-one function (i.e., multiple numbers can have the same square modulo \( p \)), the decryption process might yield two possible values for the original message. This ambiguity means there are two possible messages for each ciphertext, which is a problem in certain situations. Example: Suppose the ciphertext is \( C = 2130 \). The receiver calculates the square roots of \( C \) modulo \( p \). This process may yield two values, say \( m_1 \) and \( m_2 \), both of which could be potential original messages.
- Step 2: Handle the Ambiguity. In the Rabin Cryptosystem, decryption typically results in two possible values for the original message. The receiver needs to rely on other means (e.g., context, checksums, or error-correction codes) to figure out which one is the correct message.
Why is the Rabin Cryptosystem Secure?
- The Rabin Cryptosystem’s security is based on the quadratic residuosity problem. Given a number \( y \), it’s computationally hard to find an integer \( x \) such that: \[ x^2 \equiv y \pmod{p} \] where \( p \) is a large prime number. This makes it extremely difficult for an attacker to reverse the encryption without knowing the private key.
- The strength of the Rabin Cryptosystem comes from the fact that solving quadratic equations modulo large primes is computationally infeasible, especially as the size of \( p \) increases.
Strengths of the Rabin Cryptosystem
- Efficiency: The encryption process is very fast because squaring a number modulo a large prime is computationally efficient.
- Simplicity: The mathematical operations involved (square modulo a prime) are relatively simple compared to more complex systems like RSA.
- Theoretical Significance: It provides an alternative to RSA based on a different hard problem (quadratic residuosity).
Weaknesses of the Rabin Cryptosystem
- Decryption Ambiguity: The most significant issue is that decryption leads to two possible plaintexts. This means that the system isn’t fully reliable for general encryption unless additional measures are taken to handle this ambiguity.
- Limited Use: Due to the ambiguity in decryption, Rabin is less commonly used than RSA. It’s mainly of interest in theoretical cryptography or in special cases where the ambiguity can be managed.
- Key Size: Like RSA, Rabin requires large prime numbers for security, which increases computational costs for key generation.
Applications of the Rabin Cryptosystem
- Research in Cryptography: Though not widely used in practice, it’s an important theoretical cryptosystem in the study of number-theoretic problems and public-key cryptography.
- Hybrid Systems: Rabin could potentially be used in conjunction with other cryptosystems for specialized tasks, where its decryption ambiguity can be mitigated.
ElGamal Cryptosystem
- The ElGamal Cryptosystem is an asymmetric encryption algorithm that was introduced by Taher ElGamal in 1985. Like RSA and the Rabin Cryptosystem, ElGamal uses a pair of keys: a public key for encryption and a private key for decryption. What sets ElGamal apart is its reliance on the mathematical problem of discrete logarithms, which is a well-known mathematical problem believed to be computationally hard.
- The ElGamal system is widely used in various cryptographic applications, especially in digital signatures and public-key encryption. It is known for being probabilistic, which means it adds randomness to the encryption process, making it more secure compared to deterministic systems like RSA.
- At its core, the ElGamal Cryptosystem provides secure communication by using the principles of public-key cryptography. It works by transforming a plaintext message into ciphertext in a way that’s computationally difficult to reverse without knowing the private key.
Why is the ElGamal Cryptosystem Important?
- The ElGamal Cryptosystem is significant because it offers semantic security, which means that even if an attacker intercepts the ciphertext, they cannot gain any meaningful information about the original message without the private key.
- What makes ElGamal important?
- Security Foundation: The security of ElGamal is based on the discrete logarithm problem, which is considered difficult to solve, making the system secure.
- Versatility: ElGamal is used not only for encryption but also for creating digital signatures. This means it can be employed in a wide range of cryptographic applications.
- Foundation for Other Systems: ElGamal has laid the groundwork for other cryptographic protocols like the Digital Signature Algorithm (DSA), and is used in hybrid systems combining asymmetric and symmetric encryption techniques.
How Does the ElGamal Cryptosystem Work?
The ElGamal Cryptosystem consists of three main stages: Key Generation, Encryption, and Decryption. Each of these stages uses modular arithmetic, and it relies on the difficulty of solving the discrete logarithm problem. Let’s go through them in detail:
1. Key Generation
The first step in the ElGamal Cryptosystem is generating the public and private keys. Here’s how the key generation process works:
- Step 1: Choose a Large Prime \( p \)
- Select a large prime number \( p \), which will serve as the modulus for the system. The size of \( p \) determines the strength of the cryptosystem.
- Example: \( p = 353 \).
- Step 2: Choose a Primitive Root \( g \) Modulo \( p \)
- Select a number \( g \) (called a generator or primitive root) that is a generator of the multiplicative group of integers modulo \( p \). This means that \( g \) has the property that its powers generate all the integers from 1 to \( p-1 \) when taken modulo \( p \).
- Example: If \( p = 353 \), then \( g = 3 \) might be a valid primitive root modulo \( p \).
- Step 3: Choose a Secret Private Key \( x \)
- Select a private key \( x \), which is a secret random number. This key will be kept private by the user.
- Example: \( x = 123 \).
- Step 4: Compute the Public Key
- Calculate the public key \( h \) using the formula: \[ h = g^x \mod p \]
- The public key consists of the triplet \( (p, g, h) \), where \( p \) is the prime modulus, \( g \) is the primitive root, and \( h \) is the result of raising \( g \) to the power of the private key \( x \).
- Example:
\[
h = 3^{123} \mod 353 = 179
\]
Public Key: \( (p, g, h) = (353, 3, 179) \).
Private Key: \( x = 123 \).
2. Encryption
Once the public key is available, encryption can be done by anyone who wants to send a message securely. Here’s how encryption works:
- Step 1: Represent the Message
- Convert the message \( m \) into a number \( m \) such that \( m \) is smaller than \( p \). This can be done by converting text to ASCII codes or using other encoding schemes.
- Example: Let’s say the message \( m = 42 \).
- Step 2: Choose a Random Number \( y \)
- Select a random number \( y \) that is less than \( p-1 \). This random number adds probabilistic encryption, meaning it will make each encryption of the same message result in a different ciphertext.
- Example: \( y = 67 \).
- Step 3: Compute the Ciphertext
- The ciphertext consists of two components, \( C_1 \) and \( C_2 \), which are computed as: \[ C_1 = g^y \mod p \] \[ C_2 = m \cdot h^y \mod p \]
- \( C_1 \) is the result of raising \( g \) to the power of the random number \( y \) modulo \( p \), and \( C_2 \) is the product of the message \( m \) and \( h^y \mod p \), where \( h \) is part of the public key.
- Example: \[ C_1 = 3^{67} \mod 353 = 268 \] \[ C_2 = 42 \cdot 179^{67} \mod 353 = 144 \] The ciphertext is then \( (C_1, C_2) = (268, 144) \), which is sent to the recipient.
3. Decryption
Decryption in the ElGamal Cryptosystem is done by the receiver using their private key. Here’s how the decryption process works:
- Step 1: Compute the Shared Secret
- The receiver uses their private key \( x \) and the received \( C_1 \) to compute a shared secret \( s \) as: \[ s = C_1^x \mod p \]
- Example: \[ s = 268^{123} \mod 353 = 179 \] Notice that \( s \) is the same as \( h^y \mod p \) from the encryption step.
- Step 2: Compute the Inverse of \( s \)
- The receiver computes the modular inverse of \( s \) modulo \( p \), denoted \( s^{-1} \), which is used to recover the original message.
- Example: \[ s^{-1} = 179^{-1} \mod 353 = 319 \]
- Step 3: Recover the Original Message
- The original message \( m \) is recovered by multiplying \( C_2 \) with the inverse of \( s \): \[ m = C_2 \cdot s^{-1} \mod p \]
- Example: \[ m = 144 \cdot 319 \mod 353 = 42 \] The original message \( m = 42 \) is successfully recovered.
Why is the ElGamal Cryptosystem Secure?
- The security of ElGamal is based on the discrete logarithm problem. Given a large prime \( p \), a generator \( g \), and a number \( h = g^x \mod p \), it is computationally difficult to find the exponent \( x \) that satisfies this equation. This difficulty makes ElGamal resistant to attacks.
- The probabilistic nature of ElGamal encryption means that even if an attacker intercepts multiple ciphertexts, they cannot easily deduce any information about the messages.
Key Management
In the world of cryptography, key management is one of the most crucial aspects of securing information. It refers to the set of processes and technologies used to generate, distribute, store, use, rotate, and eventually dispose of cryptographic keys. Without effective key management, even the most advanced encryption algorithms can be rendered useless.
Think of cryptographic keys as the "passwords" that unlock encrypted data. The management of these keys is as important as the strength of the encryption itself. A weak, lost, or compromised key can jeopardize the security of an entire system. Therefore, key management ensures that keys remain safe, accessible only to authorized users, and used correctly within cryptographic protocols.
Why is Key Management Important?
- Confidentiality is maintained: No unauthorized person should access the keys.
- Integrity is preserved: Keys must not be altered or corrupted.
- Availability is ensured: Authorized users must have access to the keys when needed.
Inadequate key management can lead to:
- Data breaches if keys are stolen.
- Loss of data if keys are lost or corrupted.
- Non-compliance with industry regulations and standards like GDPR, PCI-DSS, or FIPS.
The Key Lifecycle
-
Key Generation:
- Keys are generated using secure algorithms (e.g., RSA, AES, ECC) to ensure they are random and unique.
- This process should occur in a trusted and controlled environment, often using specialized hardware like HSMs (Hardware Security Modules).
-
Key Distribution:
- Once a key is created, it needs to be securely distributed to the intended users or systems.
- For symmetric keys (e.g., AES), secure channels like Diffie-Hellman key exchange or physical transfer may be used.
- For asymmetric keys (e.g., RSA), the public key can be shared openly, but the private key must be kept secure.
-
Key Storage:
- Keys are stored in secure locations to prevent unauthorized access. This might include:
- Encrypted databases.
- Hardware Security Modules (HSMs): Devices specifically designed to generate, store, and manage cryptographic keys securely.
- Secure Enclaves or Trusted Execution Environments (TEEs) in modern processors.
-
Key Usage:
- Keys are used for encryption, decryption, signing, and verifying.
- They must be protected during use to prevent exposure in memory or to malicious programs.
-
Key Rotation:
- Regularly replacing old keys with new ones is essential for minimizing the impact of a key being compromised.
- Rotation ensures that the same key is not used indefinitely, reducing the risk of attacks like key exhaustion.
-
Key Revocation and Expiry:
- Keys should have a predefined lifespan. When a key is no longer needed or is compromised, it must be revoked.
- Revocation ensures that the key cannot be used for encryption or decryption anymore.
-
Key Destruction:
- When a key has reached the end of its lifecycle, it must be securely destroyed to prevent any chance of recovery.
- Secure methods like zeroization (overwriting memory) or physical destruction are often employed.
Key Management in Symmetric and Asymmetric Systems
-
Symmetric Key Management:
- In symmetric encryption (e.g., AES), the same key is used for encryption and decryption.
- Key management challenges:
- Key Distribution: How to securely share the key between parties.
- Key Size: Larger keys provide more security but require more storage and computational power.
-
Asymmetric Key Management:
- In asymmetric encryption (e.g., RSA, ECC), a public-private key pair is used.
- The public key is openly shared, while the private key must be kept secret.
- Key management challenges:
- Private Key Security: Protecting the private key from unauthorized access is critical.
- Key Revocation: Revoking a compromised public key requires effective communication to all users.
Key Management Techniques
- Manual Key Management:
- Suitable for small-scale applications or short-term keys.
- Keys are manually created, shared, and managed by individuals.
- Challenges: Prone to human error, scalability issues, and higher risk of key compromise.
- Automated Key Management:
- Uses software or hardware systems to manage keys throughout their lifecycle.
- Benefits:
- Reduces human error.
- Scales easily for large systems.
- Provides better logging and auditing for compliance.
- Centralized Key Management:
- All keys are managed from a single central location or system, such as a Key Management System (KMS).
- Examples: AWS KMS, Azure Key Vault, Google Cloud KMS.
- Advantages:
- Simplifies administration.
- Ensures consistent policies across the organization.
- Decentralized Key Management:
- Keys are managed locally at individual endpoints.
- Suitable for systems with highly distributed architecture.
- Challenge: Ensuring consistent policies across all nodes.
Challenges in Key Management
- Key Theft: Attackers targeting keys stored on vulnerable systems.
- Key Distribution: Securely sharing symmetric keys across untrusted networks.
- Scalability: Managing keys in large-scale systems with thousands of users or devices.
- Compliance: Meeting industry standards for encryption and key management (e.g., FIPS, GDPR, PCI-DSS).
- Backup and Recovery: Ensuring keys are backed up securely and can be recovered if lost or corrupted.
Best Practices for Key Management
- Use Secure Key Storage: Always use hardware security modules (HSMs), encrypted databases, or TEEs for storing keys.
- Enforce Strong Key Policies: Define policies for key length, rotation frequency, and expiry to align with security standards.
- Implement Multi-Factor Authentication (MFA): Add additional layers of security for accessing private keys.
- Audit Key Usage: Regularly monitor and log key usage to detect any unauthorized access or anomalies.
- Encrypt Keys: Use one key to encrypt another (key wrapping) to add another layer of protection.
- Restrict Key Access: Ensure only authorized users or systems have access to keys. Use principles like least privilege and role-based access control (RBAC).
- Plan for Key Compromise: Have a clear strategy for revoking and replacing keys in case of compromise.
Applications of Key Management
- Cloud Security: Managing encryption keys for data stored in cloud services like AWS, Azure, and Google Cloud.
- Enterprise Security: Protecting sensitive data, email communication, and network traffic in businesses.
- IoT Security: Managing keys for millions of connected devices in IoT ecosystems.
- Digital Payments: Securing transaction data in payment systems like credit cards and e-wallets.
- Secure Messaging: Protecting messages in end-to-end encrypted apps like WhatsApp or Signal.
What is Public Key Distribution?
Public Key Distribution is a process used to securely share public keys between people or systems so they can communicate securely. You might be wondering, "What’s a public key, and why do I need to distribute it?" Let’s back up a bit to understand this better.
Remember from our earlier conversation about asymmetric cryptography? In that system, there are two keys: a public key and a private key. The public key is used to encrypt messages, and the private key is used to decrypt them. The trick with public key cryptography is that you can share your public key with anyone, but you must keep your private key secret. This allows people to send you encrypted messages without needing to worry about someone intercepting the key—because the private key is only with you.
But here's the catch: To encrypt a message to you, someone needs your public key. And this is where public key distribution comes in. It’s all about making sure that the public key gets to the right person, and it happens in a way that is secure and reliable. Without it, you could give your public key to the wrong person (a hacker), and they could impersonate you or intercept your messages.
Why is Public Key Distribution Important?
When you want someone to send you a confidential message, you need them to have your public key so they can encrypt their message for you. But you can't just post your public key on a billboard or send it through a regular email—it needs to be authentic. If someone else gets a hold of your public key and pretends to be you, they could trick others into sending sensitive information to them.
So, the main goal of public key distribution is to ensure that when people get your public key, they’re sure it actually belongs to you and hasn’t been tampered with by a third party. It needs to be trusted and verified.
How Does Public Key Distribution Work?
Now that we know why it’s important, let’s look at how public key distribution happens. There are a few different methods to distribute public keys securely:
- Manual Distribution: The simplest way is for you to physically hand someone your public key. For example, if you’re meeting someone in person, you could give them a USB drive with your public key on it. This way, you control the transfer of the key, and you know it’s safe. However, this method isn’t very practical for large-scale systems or for people who are far away from each other. Plus, it doesn’t scale well.
- Public Key Infrastructure (PKI): PKI is a more sophisticated system for distributing public keys. It involves Certificate Authorities (CAs), which are trusted organizations that issue digital certificates. These certificates verify that a public key belongs to a specific person or organization. When you want to send an encrypted message to someone, you can trust the CA’s certificate to make sure the public key really belongs to the person you’re trying to communicate with. Think of it like getting a government-issued ID card. If you show your ID to someone, they know it’s authentic because the government verified it. Similarly, a CA verifies the public key’s authenticity.
- Key Servers: Another way to distribute public keys is through key servers, which are online directories where people can upload and download public keys. When you want to find someone’s public key, you can search for it on the key server. The key servers make it easy to distribute and manage public keys, but they rely on being trustworthy sources, just like the CAs. One popular system that uses key servers is PGP (Pretty Good Privacy), which is used for encrypting emails and files.
- Web of Trust: The Web of Trust is a more decentralized way of distributing public keys. Instead of relying on a central authority like a CA, individuals personally verify each other’s public keys. When you meet someone you trust, you can exchange and verify public keys directly. This can create a network of trust between individuals, forming a "web." PGP also uses this method, where users can sign each other's public keys to vouch for their authenticity.
How Do You Know a Public Key is Legitimate?
One of the challenges with public key distribution is verifying that the public key you receive is authentic. If someone intercepts a public key during distribution, they could give you their own key instead. This is where digital certificates and signature verification come into play.
- Digital Certificates: When you download a public key from a trusted source (like a CA or key server), the key is often bundled with a digital certificate. This certificate proves that the public key belongs to the person or organization that it claims to. The certificate is signed by a trusted third party, ensuring its legitimacy.
- Digital Signatures: If you’ve received a public key from someone, they can also sign the key with their private key. This helps you confirm that the key really belongs to them and hasn’t been tampered with.
What Are the Risks of Public Key Distribution?
Even though public key distribution is a great way to enable secure communication, it’s not without risks. Some potential risks include:
- Man-in-the-Middle Attacks: If an attacker intercepts your public key while it’s being sent and replaces it with their own, they could decrypt the message before passing it on to the real recipient. This is why it’s so important to use trusted methods like digital certificates or key servers for distribution.
- Fake Certificates: If a CA is compromised or unreliable, they might issue fake certificates that authenticate fraudulent public keys. This can be a big security issue, which is why many systems constantly monitor and validate the reliability of CAs.
- Key Revocation: If your private key is ever compromised, it’s crucial to revoke your public key. Public key distribution systems should have a way to revoke keys when necessary to avoid further issues.
What Are Mathematical Foundations in Cryptography?
When we talk about the mathematical foundations of cryptography, we’re referring to the basic mathematical principles and theorems that make modern cryptography work. Cryptography relies heavily on math to create secure systems for encrypting and decrypting information. Among the many mathematical tools used, number theory plays a big role because it helps us work with properties of numbers like divisibility, remainders, and modular arithmetic.
Now, two key theorems—Fermat’s Little Theorem and Euler’s Theorem—are at the heart of these foundations. They’re essential for understanding how many cryptographic algorithms, like RSA, work. So, let’s break these down step by step.
Fermat’s Little Theorem
What Is It?
Fermat’s Little Theorem is a simple yet powerful rule in number theory. It deals with prime numbers and modular arithmetic. The theorem states:
If p is a prime number and a is any integer such that a is not divisible by p, then:
ap−1 ≡ 1 (mod p)
In simpler terms:
- Take any number a.
- Raise it to the power of p−1, where p is a prime number.
- When you divide the result by p, the remainder will always be 1.
Example:
Let’s take a = 2 and p = 7 (since 7 is a prime number).
27−1 = 26 = 64
Now divide 64 by 7. The remainder is 1, so:
26 ≡ 1 (mod 7)
Why Is This Useful?
Fermat’s Little Theorem helps us work with very large numbers in cryptography. Instead of directly calculating massive powers, we can simplify them using modular arithmetic. This makes encryption and decryption processes much faster and more efficient.
Euler’s Theorem
What Is It?
Euler’s Theorem is a generalization of Fermat’s Little Theorem. It works not just for prime numbers but for any integers that are coprime (two numbers are coprime if their greatest common divisor is 1). The theorem states:
If n is a positive integer and a is an integer such that gcd(a, n) = 1, then:
aϕ(n) ≡ 1 (mod n)
Here, ϕ(n) is called Euler’s totient function, which counts the number of integers less than n that are coprime with n.
Totient Function:
- For a prime number p, ϕ(p) = p−1 (because all numbers less than p are coprime with p).
- For a composite number n = p1e1 ⋅
p2e2 ⋅ …,
ϕ(n) = n ⋅ (1−1/p1) ⋅ (1−1/p2) ⋅ ….
Example:
Let’s take n = 10 and a = 3.
- Calculate ϕ(10):
The prime factors of 10 are 2 and 5.
ϕ(10) = 10 ⋅ (1−1/2) ⋅ (1−1/5) = 10 ⋅ 1/2 ⋅ 4/5 = 4. - Apply Euler’s Theorem:
3ϕ(10) = 34 = 81.
Divide 81 by 10: The remainder is 1, so:
34 ≡ 1 (mod 10).
Why Is This Useful?
Euler’s Theorem is a cornerstone of RSA encryption, where it ensures that encryption and decryption operations work correctly. The totient function ϕ(n) plays a key role in generating secure keys.
Key Differences Between Fermat’s and Euler’s Theorems
- Scope:
Fermat’s Little Theorem applies only to prime numbers.
Euler’s Theorem applies to any positive integer n, as long as a is coprime with n. - Basis:
Fermat’s Little Theorem is a special case of Euler’s Theorem where n is a prime number. In that case, ϕ(n) = n−1.
How Are These Theorems Used in Cryptography?
- RSA Algorithm:
Both theorems help us understand how modular exponentiation works, which is the backbone of RSA. In RSA, ϕ(n) is used to generate the private and public keys securely. - Efficient Computation:
They allow us to simplify calculations involving very large numbers, which are common in cryptography. - Security:
The difficulty of reversing these calculations without the private key is what makes encryption secure.
Placement of Encryption Function
- When we talk about the placement of the encryption function, we’re essentially discussing where encryption happens in a system or network. Encryption is like wrapping a secret message in a secure envelope so no one can read it during transmission or storage. But where do you wrap that envelope? Do you do it close to the sender, somewhere in between, or closer to the receiver? The placement of the encryption function depends on various factors like security needs, system design, and how data flows in the network.
What is the Encryption Function?
- The encryption function is a process where readable data (plaintext) is transformed into unreadable data (ciphertext) using a key and an encryption algorithm. Ciphertext can only be converted back to readable plaintext by someone with the right key.
- The encryption function acts like a lock that protects the data. Its placement refers to where in the system or network this lock is applied. For instance, encryption might occur:
- On the device where the data is created (like your phone or computer).
- Somewhere in the network (such as on a server or router).
- At the destination where the data is stored or processed (like a database).
Why Does Placement Matter?
- The placement of encryption directly impacts:
- Security: The placement determines how much of the data is protected and from whom it is protected.
- Performance: Encryption takes processing power, so its placement affects the speed of the system or network.
- Cost and Complexity: Some placements require more resources, infrastructure, or coordination between components.
- Choosing the right placement ensures a balance between security, performance, and cost, tailored to the system’s needs.
Common Approaches to Placement
-
End-to-End Encryption (E2EE):
- What It Means: Encryption happens at the sender’s device, and decryption happens only at the receiver’s device. No one in between can access the data.
- Examples: Messaging apps like WhatsApp and Signal use E2EE to secure user messages.
- Advantages:
- Provides the highest level of security.
- No intermediary, such as servers or routers, can access the data.
- Disadvantages:
- Requires more processing power on devices.
- Challenging to implement in large-scale systems with multiple parties.
-
Link Encryption:
- What It Means: Encryption is applied at each link in the communication chain. Data is encrypted before transmission over a link and decrypted at the next node (e.g., a router or server), where it may be re-encrypted before moving to the next link.
- Examples: Virtual Private Networks (VPNs) often use link encryption to secure data over the internet.
- Advantages:
- Protects data from being intercepted during transmission.
- Easier to implement in networks with many nodes.
- Disadvantages:
- Data is decrypted at intermediate nodes, making it vulnerable at those points.
- Provides lower security compared to E2EE.
-
Device-Level Encryption:
- What It Means: Encryption happens directly on the device where data is created or stored. This type of encryption is often used to secure stored data rather than data in transit.
- Examples: Your smartphone’s built-in encryption protects data if the phone is stolen.
- Advantages:
- Secures data at rest (stored data).
- Protects data even if the device is lost or stolen.
- Disadvantages:
- Doesn’t protect data during transmission over a network.
-
Application-Level Encryption:
- What It Means: Encryption is applied at the application layer, typically before data is transmitted or stored.
- Examples: A payment gateway encrypting your credit card details before sending them to a server.
- Advantages:
- Provides specific control over what data is encrypted.
- Effective for protecting sensitive information like passwords or payment details.
- Disadvantages:
- Limited to protecting data within the application’s scope.
-
Network-Level Encryption:
- What It Means: Encryption is applied at the network layer to secure all data transmitted over the network.
- Examples: Protocols like HTTPS, SSL/TLS, and IPsec encrypt network traffic.
- Advantages:
- Broad protection for all data traveling over the network.
- Easier to implement for large-scale networks.
- Disadvantages:
- Doesn’t protect data at the endpoints (e.g., on sender or receiver devices).
Choosing the Right Placement
- Choosing where to place the encryption function depends on several factors:
- Type of Data: Sensitive information like passwords or personal data may require application-level encryption, while general traffic might use network-level encryption.
- Threat Model: Are you protecting against hackers on the internet, a rogue employee, or physical theft of a device?
- System Resources: Some placements, like E2EE, require more processing power, which might not always be feasible.
Real-World Use Cases
- Messaging Apps: End-to-end encryption ensures that only the sender and receiver can read the messages.
- Online Banking: Combines application-level encryption for sensitive details like passwords with network-level encryption for secure transmission.
- VPNs: Use link encryption to secure data over public networks.
- File Storage: Device-level encryption protects files stored on devices from unauthorized access.