Sequencing Problem
Meaning: The Sequencing problem involves determining an optimal order or sequence for performing a series of jobs across a number of facilities to minimize the total time or cost.
Types of Job Sequencing Problems:
- Processing n jobs through 2 machines
- Processing n jobs through 3 machines
- Processing 2 jobs through m machines
- Processing n jobs through m machines
- Processing n jobs through 1 machine
Processing n Jobs Through 2 Machines (Using Johnson's Algorithm)
Description: There are 9 jobs, each of which must be processed on Machine 1 and Machine 2 in a specific order (M1 → M2). The processing times in hours are as follows:
+------------------------------------------------------------------+
| Jobs: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
+------------------------------------------------------------------+
| Machine 1: | 5 | 3 | 12 | 15 | 6 | 10 | 11 | 9 | 5 |
+------------------------------------------------------------------+
| Machine 2: | 6 | 8 | 10 | 10 | 6 | 12 | 1 | 3 | 7 |
+------------------------------------------------------------------+
Objective: Determine a sequence for these jobs that minimizes the total elapsed time. Additionally, calculate the idle time for Machines 1 and 2.
Solution:
- Identify the optimal sequence by finding the minimum duration among Machine 1 (M1) and Machine 2 (M2).
- If the minimum duration is on M1, assign the job in forward order (left to right).
- If the minimum duration is on M2, assign the job in reverse order (right to left).
M1 ------------->
+--------------------------------------------+
| | | | | | | | | |
+--------------------------------------------+
<------------- M2
In Case of Tie:
- If a tie occurs on M1:
- Check the corresponding value on M2.
- Assign the job with the smaller M2 value first in forward order (left to right).
- If a tie occurs on M2:
- Check the corresponding value on M1.
- Assign the job with the smaller M1 value first in reverse order (right to left).
- Note: If there is still a tie after checking the opposite machine, select a job randomly.
- If the minimum value occurs on both M1 and M2 for the same job, this indicates an alternative optimal sequence is possible.
Now We Create the Optimal Job Sequence
-
The minimum value is 1, and it is from Machine 2 (M2), so assign the job in reverse
order (backward).
+--------------------------------------------+ | | | | | | | | | 7 | +--------------------------------------------+ -
The next minimum value is 3, and it is from a different machine with no tie, so
assign the job normally.
+--------------------------------------------+ | 2 | | | | | | | 8 | 7 | +--------------------------------------------+ -
The next minimum value is 5, and it appears in two places for Machine 1 (M1). We
check the corresponding values on Machine 2 (M2) and assign the job with the smaller value first.
+--------------------------------------------+ | 2 | 1 | 9 | | | | | 8 | 7 | +--------------------------------------------+ -
The next minimum value is 6, and it appears in both M1 and M2 for the same job,
leading to alternative optimal sequences.
+--------------------------------------------+ S1 | 2 | 1 | 9 | 5 | | | | 8 | 7 | +--------------------------------------------+ +--------------------------------------------+ S2 | 2 | 1 | 9 | | | | 5 | 8 | 7 | +--------------------------------------------+ -
The next minimum value is 10, and it appears in three places, but for Machine 1
(M1), it is in only one place, so we assign it first.
+--------------------------------------------+ S1 | 2 | 1 | 9 | 5 | 6 | | | 8 | 7 | +--------------------------------------------+ +--------------------------------------------+ S2 | 2 | 1 | 9 | 6 | | | 5 | 8 | 7 | +--------------------------------------------+ -
For the remaining two 10s in M2, we check their corresponding values on M1 and
assign the job with the smaller value first.
+--------------------------------------------+ S1 | 2 | 1 | 9 | 5 | 6 | 4 | 3 | 8 | 7 | +--------------------------------------------+ +--------------------------------------------+ S2 | 2 | 1 | 9 | 6 | 4 | 3 | 5 | 8 | 7 | +--------------------------------------------+ - Here, we have two optimal sequences. Either way, the total elapsed time will remain the same. For further calculations, we will use the first sequence.
Computation of Total Elapsed Time and Idle Time for Machine 1 and Machine 2
Jobs | Machine 1 || Machine 2 | Idle Time for
| Time In | Duration | Time Out || Time In | Duration | Time Out | Machine 2
------+---------+----------+----------++---------+----------+----------+---------------
2 | 0 | 3 | 3 || 3 | 8 | 11 | 3
1 | 3 | 5 | 8 || 11 | 6 | 17 | -
9 | 8 | 5 | 13 || 17 | 7 | 24 | -
5 | 13 | 6 | 19 || 24 | 6 | 30 | -
6 | 19 | 10 | 29 || 30 | 12 | 42 | -
4 | 29 | 15 | 44 || 44 | 10 | 54 | 2
3 | 44 | 12 | 56 || 56 | 10 | 66 | 2
8 | 56 | 9 | 65 || 66 | 3 | 69 | -
7 | 65 | 11 | 76 || 76 | 1 | ★77★ | 7
---------------------------------------------------------------------------------------
14
The order is Machine 1 (M1) followed by Machine 2 (M2), meaning that after a job is processed on M1, it moves to M2:
-
Important Observations:
- It is always the case that M1 Time Out ≤ M2 Time In. If not, M2 must wait until M1 finishes the job.
- The total elapsed time is 77 hours. This is the total time taken to complete all jobs through both machines, including idle time.
- Computation of Idle Time:
-
Idle time for Machine 1:
Compare the last job's time out on M1 and M2. The difference between these times is the idle time for M1.
Last job M1 Time Out = 76, Last job M2 Time Out = 77.
Difference = 1 hour.
Idle Time for Machine 1 = 1 hour. -
Idle time for Machine 2:
The idle time for M2 is calculated as follows:- For the first job, the time out of M1 becomes the idle time for M2.
- For subsequent jobs, the idle time is the difference between M2's time in and the previous job's time out, if any.
Total Idle Time for Machine 2 = 14 hours.
-
Idle time for Machine 1:
Processing n Jobs Through Three Machines
Question: There are five jobs, each of which needs to be processed sequentially through three machines: A, B, and C. The processing order for each job is A → B → C. The processing times (in minutes) for the jobs on each machine are given below:
Job | A | B | C
----+----+----+----
1 | 6 | 8 | 14
2 | 16 | 10 | 18
3 | 14 | 2 | 10
4 | 10 | 4 | 12
5 | 8 | 6 | 20
Objective: Determine the following:
- The optimum sequence for processing the five jobs to minimize total processing time.
- The minimum elapsed time required to complete all jobs.
- The idle time for each machine (time when a machine is not processing any job).
- The waiting time for each job (time spent waiting for a machine to become available).
Solution:
Step 1: Check the conditions
-
Minimum duration of Machine A should be ≥ Maximum duration of Machine B.
Condition: Min A ≥ Max B -
Minimum duration of Machine C should be ≥ Maximum duration of Machine B.
Condition: Min C ≥ Max B
If either or both of the above conditions are satisfied, proceed to the next step. Otherwise, the algorithm fails.
-
First, find the relevant durations:
Minimum duration of Machine A = 6
Minimum duration of Machine C = 10
Maximum duration of Machine B = 10 -
Check the conditions:
1 → Min A ≥ Max B?
6 ≥ 10 ✗
2 → Min C ≥ Max B?
10 ≥ 10 ✓ - Since one condition is satisfied, we can proceed further.
Step 2: Introduce two fictitious (imaginary) machines M1 and M2.
- Define M1 = [A + B] and M2 = [B + C].
Job | M1 | M2
| [A+B] | [B+C]
----+-------+------
1 | 14 | 22
2 | 26 | 28
3 | 16 | 12
4 | 14 | 16
5 | 14 | 26
- Using Johnson's Algorithm for n jobs through 2 machines, determine the optimum sequence.
+-----------------------+
Optimum Sequence | 4 | 1 | 5 | 2 | 3 |
+-----------------------+
Apply this optimal sequence to the original problem:
Computation of Minimum Elapsed Time
Jobs | Machine A || Machine B || Machine C |
| Time | D | Time || Time | D | Time || Time | D | Time |
| In | | Out || In | | Out || In | | Out |
------+------+----+------++------+----+------++------+----+------+
4 | 0 | 10 | 10 || 10 | 4 | 14 || 14 | 12 | 26 |
1 | 10 | 6 | 16 || 16 | 8 | 24 || 26 | 14 | 40 |
5 | 16 | 8 | 24 || 24 | 6 | 30 || 40 | 20 | 60 |
2 | 24 | 16 | 40 || 40 | 10 | 50 || 60 | 18 | 78 |
3 | 40 | 14 | 54 || 54 | 2 | 56 || 78 | 10 | ★88★ |
- Minimum elapsed time = 88 minutes.
-
Finding idle time:
-
Idle time for Machine A:
Compare minimum elapsed time and last job's time out.
54 and 88.
Idle time = 88 - 54 = 34 minutes. -
Idle time for Machine B:
First idle time = 10.
During processing = 2 + 10 + 4 = 16.
Total till now = 10 + 16 = 26
Last job's out time = 56.
Elapsed time = 88.
Total idle time = 26 + (88 - 56) = 58 minutes. -
Idle time for Machine C:
First idle time = 14.
During processing = 0.
Total idle time = 14 minutes.
-
Idle time for Machine A:
-
Waiting time for jobs:
Calculate the time difference between a job's out time on one machine and its in time on the next machine.
Job 4: 0 minutes
Job 1: 2 minutes
Job 5: 10 minutes
Job 2: 10 minutes
Job 3: 22 minutes
Total waiting time = 44 minutes.
Processing 2 Jobs through m Machines
These types of problems can only be solved using graphical methods.
Question: Using the graphical method, determine the optimal sequence needed to process Job 1 and Job 2 on five machines (A, B, C, D, and E). For each machine, find the job which should be done first. Also, calculate the total time needed to complete both jobs.
Job 1
Sequence : A B C D E
Time (hrs) : 3 4 2 6 2
Job 2
Sequence : B C A D E
Time (hrs) : 5 4 3 2 6
Solution:
Step 1: Plot the graph using the given information.
- Job 1 will be on the x-axis, and Job 2 will be on the y-axis.
- Calculate the total hours to plot the axes:
For Job 1: 3 + 4 + 2 + 6 + 2 = 17
For Job 2: 5 + 4 + 3 + 2 + 6 = 20 - Also, lay out the machine times for the two jobs on their respective axes.
- For the first machine (A): Job 1 duration = 3 hrs. Check the same machine's duration for Job 2
and construct a square or rectangle at the common area.
Find the intersecting area for Machine A for Job 1 and Job 2. - After plotting the graph, identify the finish points:
Job 1: Finish at 17
Job 2: Finish at 20
Hence, the finish point is (17, 20).
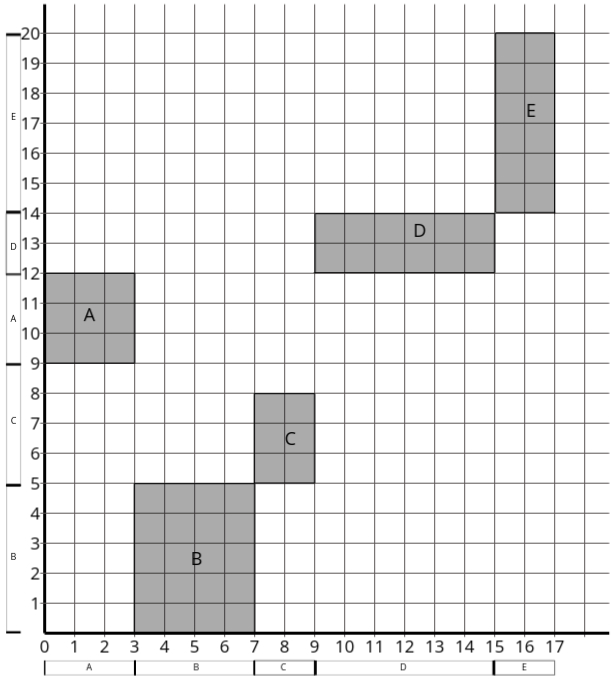
Step 2: Calculate the total elapsed time for Job 1 and Job 2 (including idle time).
- Draw two types of lines:
- A 45° diagonal line representing simultaneous processing of the two jobs on different machines.
- Horizontal and vertical lines representing idle times.
- Start at (0, 0) and move through the five machines for Job 1 and Job 2, avoiding lines passing through rectangles or squares.
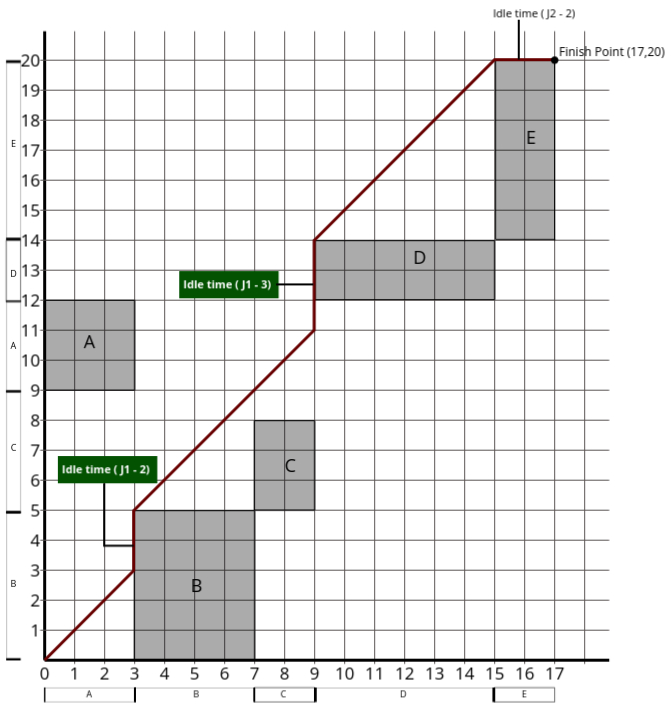
- Total Elapsed Time:
For Job 1: Actual finish time (17) + Idle time (5) = 22
For Job 2: Actual finish time (20) + Idle time (2) = 22 - Observations:
- The 45° diagonal line represents simultaneous processing of the two jobs on different machines.
- The graph has:
- Two vertical lines representing idle time for Job 1.
- One horizontal line representing idle time for Job 2.
- Idle time durations:
First vertical line: 2
Second vertical line: 5
Total vertical idle time: 5
Horizontal idle time: 2
Optimal Schedule
The optimal schedule is constructed by combining actual time and idle time into a timeline.
Job 1
IT = Idle Time
| 3 | 2 | 4 | 3 | 3 | 6 | 2 |
| A | IT | B | C | IT | D | E |
+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
Job 2
| 5 | 4 | 3 | 2 | 6 | 2 |
| B | C | A | D | E | IT |
+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+---+
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
The optimal schedule on various machines for Job 1 and Job 2:
Machine A: J1 then J2
Machine B: J2 then J1
Machine C: J2 then J1
Machine D: J2 then J1
Machine E: J2 then J1
Processing N Jobs through M Machines
Question:Four jobs 1, 2, 3 and 4 are to be processed on each of the five machines A, B, C, D and E in the order ABCDE. Find the toal minimum elapsed time if no passing of jobs is permitted. Also determine idle time for each machine
Machine →| A | B | C | D | E
Jobs ↓ | | | | |
---------------------------------------------
1 | 14 | 10 | 4 | 6 | 18
2 | 12 | 12 | 8 | 10 | 20
3 | 10 | 8 | 10 | 12 | 16
4 | 16 | 6 | 6 | 4 | 12
Solution:
- In order to solve the problem the fist step is - we nned to find minimum duration of first
machine & last machine
For A = 10
For E = 12 - Now we need to find maximum duration for each machines which are b/w fisrt and last
B max = 12
C max = 10
D max = 12 - Now we need fo ind the maximum duration among betweein fist and last so here B, C, D
so the max in B, C, D is = 12 - Now we check the condition:
- Min A >= Max[B, C, D]
- Min E >= Max [B, C, D]
(2) >= 12 ✓ - If both the condition are not satisfied then we can't solve this problem
- Next we find the optimal sequcnec for that we convert those 5 macines to 2 machines
Machine a = add up all duration except lsat one (A + B + C + D)
Machine b = add up all except first one (B + C + D + E)
Job | Machine a | Machine b
| [A + B + C + D] | [B + C + D + E]
-------------------------------------------
1 | 34 | 38
2 | 42 | 50
3 | 40 | 46
4 | 32 | 28
- Now using Johnson's Method we find Optimal Sequence.
+------------------+
| 1 | 3 | 2 | 4 |
+------------------+
Now we find the elapsed time and idle time for each machine
Jobs | Machine A || Machine B || Machine C || Machine D || Machine E |
| Time | D | Time || Time | D | Time || Time | D | Time || Time | D | Time || Time | D | Time |
| In | | Out || In | | Out || In | | Out || In | | Out || In | | Out |
------+------+----+------++------+----+------++------+----+------++------+----+------++------+----+------+
1 | 0 | 14 | 14 || 14 | 10 | 24 || 24 | 4 | 28 || 28 | 6 | 34 || 34 | 18 | 52 |
3 | 14 | 10 | 24 || 24 | 8 | 32 || 32 | 10 | 42 || 42 | 12 | 54 || 54 | 16 | 70 |
2 | 24 | 12 | 36 || 36 | 12 | 48 || 48 | 8 | 56 || 56 | 10 | 66 || 70 | 20 | 90 |
4 | 36 | 16 | 52 || 52 | 6 | 58 || 58 | 6 | 64 || 66 | 4 | 70 || 90 | 12 |★102★ |
- 102 is minimum elapsed time
- Idle time on machine
A = 102 - 52 = 50
B = 14 + 4 + 4 + (102-58) = 66
C = 24 + 4 + 6 + 2 + (102 - 64) = 74
D = 28 + 8 + 2 + (102 - 70) = 70
E = 34 + 2 = 36