Backpropagation Neural Network (BPN)

• It is a standard method for training Artificial Neural Networks (ANNs).
• BPN is a method of continuously adjusting the weights of the connections in the network to minimize the difference between the actual output and the desired output. This method aims to find the minimum value of the error in the weight space using the delta rule of gradient descent.

Steps in BPN:

1. Input x is introduced to the network through pre-connected paths.
2. Inputs are modeled using randomly assigned weights w.
3. Calculate the output of each neuron, propagating from the input layer to the hidden layer, and then to the output layer.
4. Calculate the error at the output layer. The error can be computed as the difference between the actual output and the desired output (i.e., Error = Actual Output - Desired Output).
5. The error is then propagated backward, from the output layer to the hidden layer, and then back to the input layer. The weights are adjusted at each layer to reduce the error. This process is repeated iteratively until the error is minimized.

Confusion?

• Even though backpropagation involves "going backward," this backward flow occurs only during the training phase. The backpropagation algorithm computes the gradients of the error with respect to each weight in the network by working backward, but this process is purely for adjusting the weights and is not part of the actual inference or data flow during prediction.
• Thus, during inference or the actual operation of the network (when you're making predictions), the data still flows strictly in the forward direction—from inputs to outputs. This is why networks trained using backpropagation are still considered feedforward networks. The term "feedforward" refers to how information is processed when the network is used for predictions, not how it learns.
• BPN ko feedforward network ke under isliye include karte hain kyunki backward direction sirf training ke time pe hota hai. Jab hum network ko train karte hain, tab error ko piche ki taraf propagate karke weights adjust karte hain. Lekin jab actual prediction karte hain, yaani jab hum model ko real data dete hain, toh data sirf forward direction mai flow hota hai—input se output tak.
  Yeh jo term 'feedforward' hai, yeh sirf prediction ke process ke baare mein hai, training ke time pe kya hota hai, usse nahi. Isliye, BPN ko feedforward neural network mana jata hai, kyunki prediction ke waqt data forward hi move karta hai.

Example Problem: Assume that the neurons have a sigmoid activation function, perform a forward pass and a backward pass on the network. Assume that the actual output of y is 0.5 and learning rate is 1.

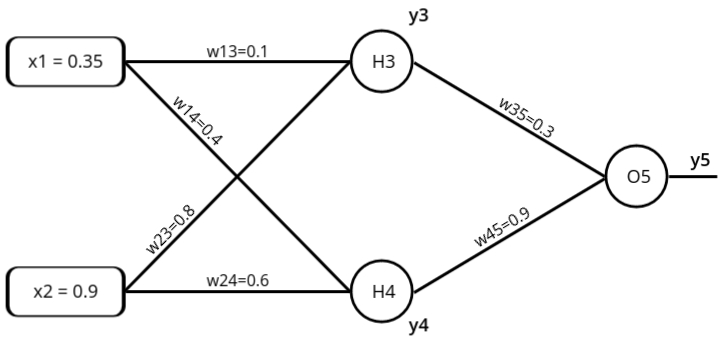
Forward Pass: Compute output for y₃, y₄ and y₅.

• a_j = \( \sum_{j} (w_ij * x_i) \)

y_j = f(aj) = \( f(x) = \frac{1}{1 + e^{-a_j}} \)
• y₃ = f(a1) = \( f(a1) = \frac{1}{1 + e^{-a_1}} \)
  a1 = (w₁₃ * x₁ ) + (w₂₃ * x₂) = 0.755
  y₃ = f(0.755) = \( f(a1) = \frac{1}{1 + e^{-0.755}} \) = 0.68
• y₄ = f(a2) = \( f(a2) = \frac{1}{1 + e^{-a_2}} \)
  a2 = (w₁₄ * x₁ ) + (w₂₄ * x₂) = 0.68
  y₄ = f(0.68) = \( f(a1) = \frac{1}{1 + e^{-0.68}} \) = 0.6637
• y₅ = f(a3) = \( f(a3) = \frac{1}{1 + e^{-a_1}} \)
  a3 = (w₃₅ * y₃ ) + (w₄₅ * y₄) = 0.801
  y₅ = f(0.801) = \( f(a3) = \frac{1}{1 + e^{-0.801}} \) = 0.69
• Error = y_target - y₅ = -0.19

To get closure to the desired output we need to update the weight.

Each Weight changed by:

• Δw_ij = ηδ_jO_i
  • δ_j = O_j(1 - O_j)(t_j - O_j) if j is an output unit
  • δ_j = O_j(1 - O_j)\( \sum_{k}\)δ_kw_kj if j is a hidden unit
• where η is a constant called the learning rate
• t_j is the correct output for unit j
• δ_j is the error measure for unit j
• O_i represents the output of the unit i in the previous layer. In the case of a hidden or output unit, it refers to the activation value of that unit.

Backward Pass: Compute δ₃, δ₄ and δ₅

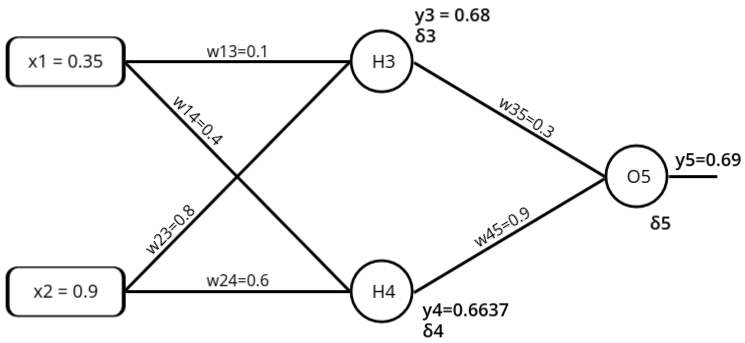
• For output unit:
  δ₅ = y₅(1-y₅)(y_target - y₅)
  = 0.69*(1-0.69)*(0.5-0.69) = -0.0406
• For hidden unit:
  δ₃ = y₃(1-y₃)w35*δ₅
  0.68*(1-0.68)*(0.3*(-0.0406)) = -0.00265
• For hidden unit:
  δ₄ = y₄(1-y₄)w45*δ₅
  0.6637*(1-0.6637)*(0.9*(-0.0406)) = -0.0082

Compute new weights

Δw_ij = ηδ_jO_i

• Δw₁₃ = ηΔ₃x₁ = 1 * (-0.00265) * 0.35 = −0.0009275
  Δw₁₃(new) = Δw₁₃ + w₁₃(old) = −0.0009275 + 0.1 = 0.0991
• Δw₁₄ = ηΔ₄x₁ = 1 * (-0.0082) * 0.35 = -0.00287
  Δw₁₄(new) = Δw₁₄ + w₁₄(old) = -0.00287 + 0.4 = 0.3971
• Δw₂₃ = ηΔ₃x₂ = 1 * (-0.00265) * 0.9 = -0.002385
  Δw₂₃(new) = Δw₂₃ + w₂₃(old) = -0.002385 + 0.4 = 0.7976
• Δw₂₄ = ηΔ₄x₂ = 1 * (-0.0082) * 0.9 = -0.00738
  Δw₂₄(new) = Δw₂₄ + w₂₄(old) = -0.00738 + 0.6 = 0.5926
• Δw₃₅ = ηΔ₅y₃ = 1 * (-0.0406) * 0.68 = -0.0276
  Δw₃₅(new) = Δw₃₅ + w₃₅(old) = -0.0276 + 0.3 = 0.2724
• Δw₄₅ = ηΔ₅y₄ = 1 * (-0.0406) * 0.6637 = -0.0269
  Δw₄₅(new) = Δw₄₅ + w₄₅(old) = -0.0269 + 0.9 = 0.8731

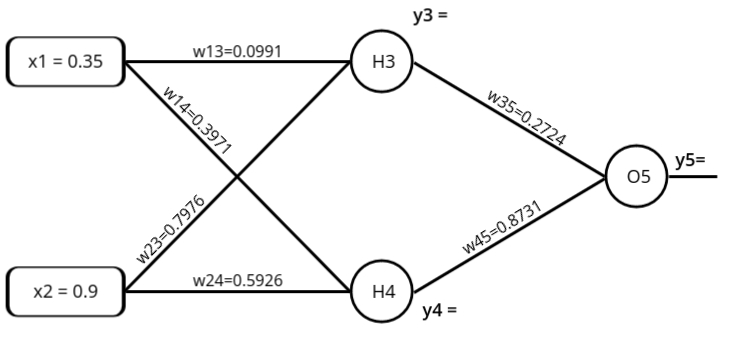
Forward Pass: Compute output y₃, y₄ and y₅.

• y₃ = f(a1) = \( f(a1) = \frac{1}{1 + e^{-a_1}} \)
  a1 = (w₁₃ * x₁ ) + (w₂₃ * x₂) = 0.7525
  y₃ = f(0.7525) = \( f(a1) = \frac{1}{1 + e^{-0.7525}} \) = 0.6797
• y₄ = f(a2) = \( f(a2) = \frac{1}{1 + e^{-a_2}} \)
  a2 = (w₁₄ * x₁ ) + (w₂₄ * x₂) = 0.6797
  y₄ = f(0.6797) = \( f(a1) = \frac{1}{1 + e^{-0.6797}} \) = 0.6620
• y₅ = f(a3) = \( f(a3) = \frac{1}{1 + e^{-a_1}} \)
  a3 = (w₃₅ * y₃ ) + (w₄₅ * y₄) = 0.7631
  y₅ = f(0.7631) = \( f(a3) = \frac{1}{1 + e^{-0.7631}} \) = 0.6820 (Network Output)
• Error = y_target - y₅ = -0.182

Radial Basis Function Network (RBFN)

What is an RBFN?
A Radial Basis Function Network (RBFN) is a type of artificial neural network that uses radial basis functions (RBFs) to map input data into an output. It’s mainly used for classification, regression, and function approximation. The network is especially useful for handling non-linear data, where relationships between the inputs and outputs are not simple and straight-forward.

How Does an RBFN Work?

RBFNs have a simple but powerful design that works in three main layers. Let's break down each part:

• Three-Layer Structure: RBFNs are built with three layers:
  • Input Layer: The input layer receives the raw data (e.g., features or numbers).
  • Hidden Layer: This is where the magic happens. The hidden layer neurons have specific "centers" that measure how far the input data is from the center. This is done using a radial basis function (e.g., the Gaussian function).
  • Output Layer: This layer gives the final result. The weighted sum of the values from the hidden layer is passed here to produce the output.
• Using Distance for Classification: The key idea behind RBFNs is that each neuron in the hidden layer has a "center point." When new input comes in, the network calculates how far the input is from these centers. The closer the input is to a center, the stronger the output signal. This helps the network classify or predict outputs based on these distances.

Training an RBFN

Now that we know how the network is structured, let's talk about how the network learns and adjusts:

• Step 1: Find the Centers: The centers of the hidden layer neurons are first chosen. This can be done using methods like k-means clustering, which groups similar inputs together and identifies the center of each group.
• Step 2: Adjust the Weights: After determining the centers, the network adjusts the weights between the hidden and output layers. These weights are fine-tuned using methods like gradient descent or least squares, helping the network learn how to make accurate predictions.

Why Use RBFNs?

RBFNs are particularly useful for solving complex problems because of their ability to handle non-linear relationships. Here’s why they stand out:

• Handles Non-Linear Data: RBFNs are great for problems where the relationship between inputs and outputs isn't linear. They can transform complex, non-linear data into a form that is easier to model.
• Fast Training: RBFNs often train faster than other neural networks because the network only needs to adjust the weights between the hidden and output layers, not the centers.
• Good for Function Approximation: RBFNs are good at approximating unknown functions, making them ideal for tasks like time-series prediction, forecasting, and control systems.

Real-Life Example: Predicting House Prices

Let’s say you want to predict the price of a house based on features like location, size, and number of bedrooms. An RBFN works by calculating the distance between these input features and learned "center" points from similar houses, then giving you a price prediction. It’s particularly good when the relationship between the features and the price isn’t simply linear, like if the price increases disproportionately with location or size.

Hopfield Network

The Hopfield Network is a type of neural network used for remembering patterns and retrieving them when given incomplete or noisy information. Think of it like your brain recognizing a friend’s face even if they’re wearing sunglasses or a hat.

Key Concepts:

• Neurons and States: The Hopfield network is made up of simple units called neurons. Each neuron can have only two states: on or off (typically represented as +1 and -1).
• Connections Between Neurons: Every neuron is connected to every other neuron, but not to itself. These connections have weights, which decide how strongly one neuron influences another.
• Pattern Storage: The Hopfield network can store patterns (like pictures, sounds, or any data). Once it learns a pattern, it can recall it from partial or distorted input. For example, if the network is trained to remember a face, it can still recognize it even if the face is blurry.
• How the Network Works:
  • Learning: The Hopfield network learns by adjusting the weights between neurons based on the patterns you give it. This process ensures that the network can later recall these patterns.
  • Recall: When you give the network a part of a pattern (like a blurry version of a face), it updates the neuron states until it matches the closest pattern it remembers. This process happens in small steps, one neuron at a time.
• Stable States: A Hopfield network has special stable states, called attractors. Once the network reaches a stable state, it stops changing. These stable states correspond to the patterns it has learned.
• Energy Minimization: Hopfield networks work by trying to minimize an "energy" function. This means the network always moves towards a more stable pattern, just like a ball rolling downhill until it reaches the bottom.

Why Use Hopfield Networks?

• They are great for associative memory, where you want to remember something based on partial input.
• They’re used in pattern recognition, such as recognizing handwriting, faces, or other types of data.

Real-World Example

Imagine you give a Hopfield network a picture of a cat to remember. Later, you give it a blurry or incomplete version of the cat, and the network will fill in the missing details to recall the full image.

Bidirectional Associative Memory (BAM)

Bidirectional Associative Memory (BAM) is a type of neural network that links two sets of patterns together, so you can recall one pattern if you know the other. It works by associating pairs of patterns, and it can retrieve one pattern from either side of the pair. This makes it useful for situations where two different patterns are connected, like matching translations between two languages or linking two related items.

Key Concepts

• Bipolar Neurons: BAM uses neurons that can only have two possible states: +1 (on) or -1 (off). These simple states are used to represent the presence or absence of a particular pattern.
• Two Layers: BAM has two separate layers of neurons, which are the X layer and the Y layer. Each layer contains a pattern, and the neurons in the X layer are connected to neurons in the Y layer. These layers are designed to hold different patterns that are related to each other.
• Bidirectional Recall: BAM is special because it can recall the corresponding pattern from the opposite layer. For example, if you input a pattern into the X layer, BAM will find the matching pattern in the Y layer. Similarly, if you provide a pattern to the Y layer, BAM can recall the matching pattern from the X layer. This bidirectional linking is key to BAM’s functionality.

How BAM Works

• Learning Process: BAM learns by adjusting the strength of connections between the neurons in the X and Y layers. When BAM is given a pair of patterns, one pattern in the X layer and the corresponding pattern in the Y layer, the network strengthens the connections between neurons that represent these patterns. This enables BAM to recall the patterns later when given part of either pattern.
• Recall Process: Once BAM has learned the associations between the patterns, it can recall the complete pattern if given an incomplete or partial input. For example, if you input part of the pattern from the X layer, BAM will use its learned connections to retrieve the corresponding pattern from the Y layer, and vice versa. This is done through a process of updating the states of the neurons until the most likely matching pattern is found.

Why Use BAM?

• BAM is great for pattern association, where you need to link two sets of patterns together. For example, in machine translation, BAM can associate words in one language with their equivalent words in another language.
• It’s also useful in applications where data comes in pairs and needs to be recalled together, such as in image recognition or data retrieval systems where knowing one piece of information helps you retrieve the other.

Real-World Example

Imagine you train BAM to link English words with their French translations. If you input the word "dog" into the X layer, BAM will recall the French word "chien" in the Y layer. On the other hand, if you input "chien" into the Y layer, BAM will recall "dog" in the X layer. This bidirectional recall makes BAM useful for language translation tasks where you need to recall one translation after knowing the other.

Self-Organizing Maps (SOM)

Self-Organizing Maps (SOM) are a type of neural network used for organizing and visualizing data without needing labels. They group similar data together, making it easier to understand patterns, especially in high-dimensional data. Think of it like sorting a pile of mixed items into categories based on their similarities, but without knowing what categories to expect in advance.

Key Concepts

• Unsupervised Learning: SOM is an unsupervised learning algorithm, meaning it doesn't need labeled data. It learns by finding similarities in the input data and organizing them accordingly.
• Topological Map: The SOM creates a 2D map, where similar data points are placed close to each other, allowing you to see patterns in the data visually.
• Neurons and Grid: The network consists of a grid of neurons, each representing a group of similar data points. Each neuron adjusts its “weight” (value) to match the input data during training.

How SOM Works

• Training: SOM is trained by presenting input data repeatedly. The neurons adjust their weights to better match the data. With each step, the neurons closest to the input data change more.
• Best Matching Unit (BMU): The neuron that is closest to the input data (based on its weight) is called the Best Matching Unit (BMU). This neuron and its neighbors adjust their weights to match the input better.
• Neighborhood Function: The adjustment happens not just at the BMU, but also in nearby neurons. Neurons that are closer to the BMU adjust more, helping to group similar data together in the map.

Why Use SOM?

• Data Visualization: SOM is great for turning complex, high-dimensional data into a simple 2D map, making patterns easier to see.
• Clustering: It’s useful for clustering similar data points together, even when you don't know the groups in advance.
• Dimensionality Reduction: SOM reduces the complexity of data while maintaining its structure, making analysis easier.

Real-World Example

Imagine you have data on customers’ shopping habits, including information like age, income, and products bought. A SOM can group customers with similar behaviors together. After training, you can visualize these customer groups on a 2D map, where similar customers are close to each other, helping you find patterns and insights.

Learning Vector Quantization (LVQ)

Learning Vector Quantization (LVQ) is a supervised learning algorithm used for classification tasks. It groups data into categories using prototypes, which are reference points that represent different classes. When a new input comes in, LVQ finds the closest prototype and assigns it to the corresponding category.

Key Concepts

• Supervised Learning: LVQ is supervised, meaning it learns from labeled data to classify new inputs into predefined categories.
• Prototypes: Prototypes are the reference points that represent classes in the data. They are adjusted during training to improve classification accuracy.
• Winner-Takes-All Rule: When an input is presented, the closest prototype (the "winner") is updated to better match the input, strengthening its class representation.

How LVQ Works

• Initialization: Start with a set of prototypes representing the different classes in the training data.
• Training: The network presents input vectors, and the closest prototype is selected. Prototypes are adjusted based on whether they represent the correct class or not.
• Prototype Adjustment: Correct prototypes move closer to the input data, while incorrect prototypes move further away, reducing classification errors.

Why Use LVQ?

• Simple and Interpretable: LVQ is easy to understand and visualize, as the classification boundaries are based on prototypes.
• Effective for Classification: It works well for problems where data can be clustered into clear categories.
• Versatile: LVQ can be applied to many types of classification tasks, like image recognition or medical diagnosis.

Real-World Example

Imagine classifying flowers based on features like petal length and width. LVQ would create prototypes for different flower types (e.g., roses, lilies). As the network learns, these prototypes adjust to better represent each flower type, enabling accurate classification of new flowers.